- #1
Juntao
- 45
- 0
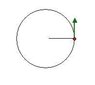
A child is playing with a ball on a string. The ball has mass 0.065 kg, the string has radius 1.2 m and assume that the string is massless. The child swings the ball on a string in a vertical circle. Halfway up the circle the speed of the ball is measured to be 8.7 m/s. What is the maximum tension in the string?
I know that a=V^2/R
F=MV^2/R
And since I'm working in the work-energy chapter this week, I think maybe I could apply the work energy theorem to this problem, but not sure how or even how to start this problem.
So help greatly appreciated.
I know that a=V^2/R
F=MV^2/R
And since I'm working in the work-energy chapter this week, I think maybe I could apply the work energy theorem to this problem, but not sure how or even how to start this problem.
So help greatly appreciated.