- #1
Chris L T521
Gold Member
MHB
- 915
- 0
Thanks again to those who participated in last week's POTW! Here's this week's problem!
-----
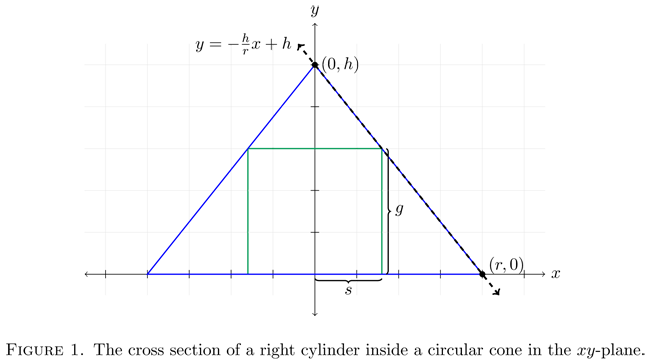
Problem: A right circular cylinder is inscribed in a cone with height $h$ and base radius $r$. Find the largest possible volume of such a cylinder.
-----
-----
Problem: A right circular cylinder is inscribed in a cone with height $h$ and base radius $r$. Find the largest possible volume of such a cylinder.
-----