- #1
Aerospace
- 39
- 0
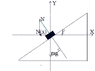
Q1. A 3.87 kg block is held in equilibrium on an incline by the horizontal force F. The incline makes a 23.6 degree angle with the horizontal. Determine the magnitude of F. Answer in units of N.
Q2. The distance between two telephone poles is 48 m. When a 1.36 kg bird lands on the telephone wire midway between the poles, the wire sags 0.118 m. how much tension in the wire does the bird produce? Ignore the weight of the wire. Answer in units of N.
--
We haven't covered these topic yet in my class, and there's not much in the book that is helping me since the homework assignment is based on a different book that the prof used last year. If you guys could give me some directions as to how to go about solving these questions - if I get these, I'm sure I'll get most of the Qs - if not all.
Q2. The distance between two telephone poles is 48 m. When a 1.36 kg bird lands on the telephone wire midway between the poles, the wire sags 0.118 m. how much tension in the wire does the bird produce? Ignore the weight of the wire. Answer in units of N.
--
We haven't covered these topic yet in my class, and there's not much in the book that is helping me since the homework assignment is based on a different book that the prof used last year. If you guys could give me some directions as to how to go about solving these questions - if I get these, I'm sure I'll get most of the Qs - if not all.