- #1
taishizhiqiu
- 63
- 4
I have been reading about Z2 topological invariant recently. However, after some literature survey, I still cannot understand Z2 invariant in language of time reversal polarization.
Basically, my struggle includes the following two questions:
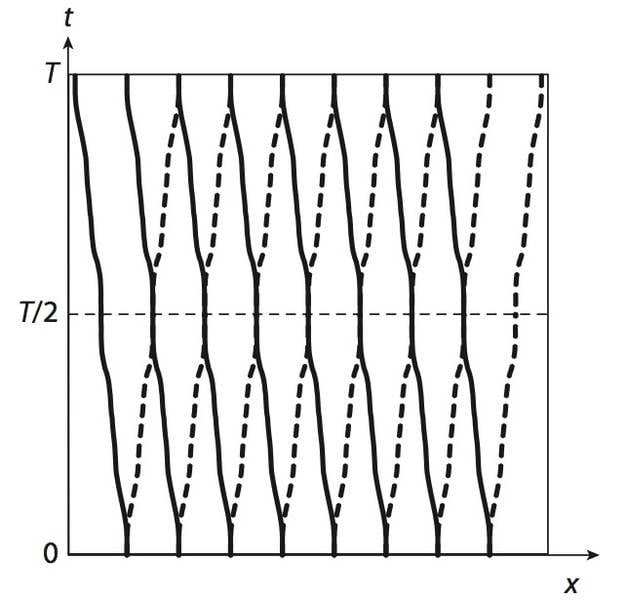
(ref http://link.aps.org/doi/10.1103/PhysRevB.74.195312)
Basically, my struggle includes the following two questions:
- As the ref paper says(see the picture below): On the edge, however, partner switching results in the occupied Wannier orbital at t = 0 switching partners and having as a partner at t = T/2, a formerly unoccupied Wannier orbital. If we consider a two band system for simplicity(one occupied valence band and one empty conduction band), all wannier states of valence band are occupied and where is this formerly unoccupied Wannier orbital? Is this a Wannier orbital from conduction band?
- Still, why such a partner switching will result in an edge state connecting valence and conduction band in quantum spin hall effect(with ##k_y## acting as ##t##)?
(ref http://link.aps.org/doi/10.1103/PhysRevB.74.195312)