- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Tristan Needham's book "Visual Complex Analysis" and am currently focussed on Chapter 1, Section II Euler's Formula ... in particular I am trying to follow Needham's heuristic argument in support of, or justifying, Euler's formula - Needham calls it 'the moving particle argument' ... ...
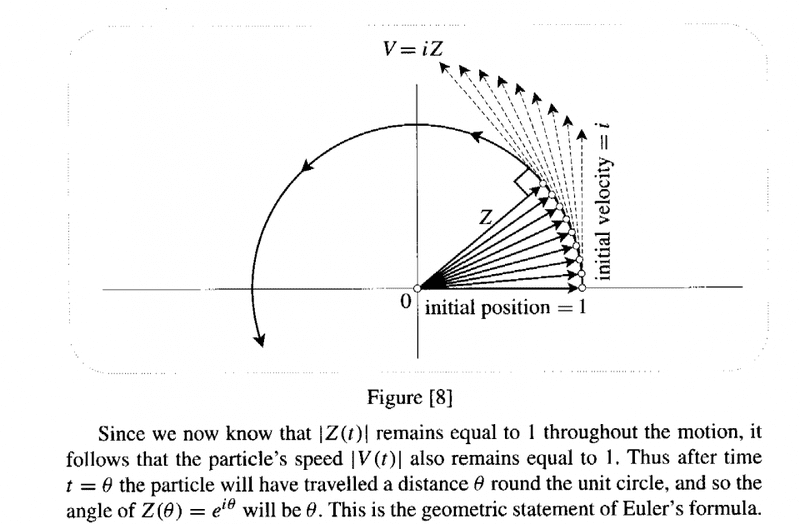
In Chapter 1, Section II (2), Needham considers a particle moving along a curve:
##Z(t) = e^{it}##
So he finds that:
## \frac{dZ}{dt} = ie^{it} = iZ ##
Needham then argues that each new velocity, instant by instant, will be at right angles to its new position vector ( ? ... presumably because the function ##iZ## causes a rotation of 90 degrees - is that right? ... ) ...
He then asserts that "it is clear" that the particle will travel around a unit circle ... ... BUT ... ... why exactly is this the case? ... ... indeed, how do we rigorously prove that this is the case? ... ...
The relevant part of Needham's text is as follows:


Now ... just a further question based on a claim in the last paragraph above ... ...
Needham writes:
" ... ... Thus after time ##t = \theta## the particle will have traveled a distance ##\theta## round the unit circle, and so the angle of ##Z( \theta ) = e^{i \theta }## will be ##\theta##. This is the geometric statement of Euler's formula ... ... "My question is ... ... in what way ... that is how/why is this the geometric statement of Euler's formula ... ...
Help will be appreciated ...
Peter
In Chapter 1, Section II (2), Needham considers a particle moving along a curve:
##Z(t) = e^{it}##
So he finds that:
## \frac{dZ}{dt} = ie^{it} = iZ ##
Needham then argues that each new velocity, instant by instant, will be at right angles to its new position vector ( ? ... presumably because the function ##iZ## causes a rotation of 90 degrees - is that right? ... ) ...
He then asserts that "it is clear" that the particle will travel around a unit circle ... ... BUT ... ... why exactly is this the case? ... ... indeed, how do we rigorously prove that this is the case? ... ...
The relevant part of Needham's text is as follows:
Now ... just a further question based on a claim in the last paragraph above ... ...
Needham writes:
" ... ... Thus after time ##t = \theta## the particle will have traveled a distance ##\theta## round the unit circle, and so the angle of ##Z( \theta ) = e^{i \theta }## will be ##\theta##. This is the geometric statement of Euler's formula ... ... "My question is ... ... in what way ... that is how/why is this the geometric statement of Euler's formula ... ...
Help will be appreciated ...
Peter
Attachments
Last edited:



 ) to work out the solution to the differential equation ##dy/dθ = iy##
) to work out the solution to the differential equation ##dy/dθ = iy##