- #1
Guillem_dlc
- 184
- 15
- Homework Statement
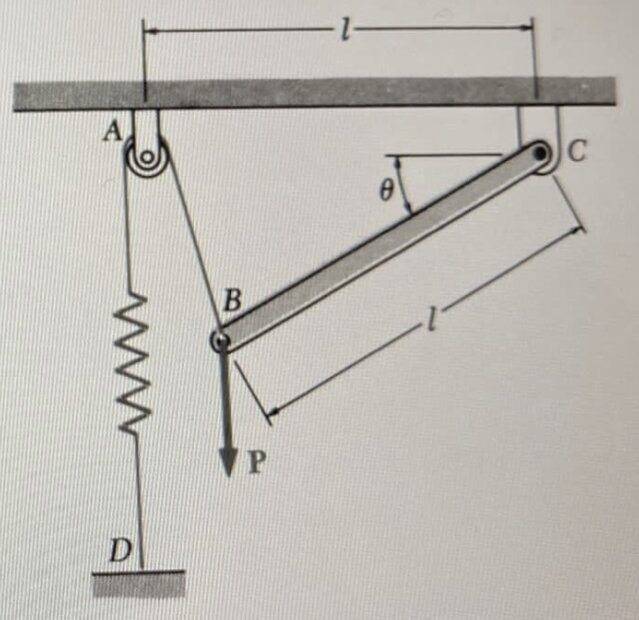
- At the end ##B## of rod ##BC## a vertical load ##P## is applied. The spring constant is ##k## and it forms an angle ##\theta=0## when the spring is unstretched.
a) Neglecting the weight of the rod, express the angle ##\theta## corresponding to the equilibrium position in terms of ##P##, ##k## and ##l##. Sol: ##\theta =\arctan \dfrac{P}{kl}##
b) Determine the value of ##\theta## corresponding to equilibrium if ##P=2kl##. Sol: ##\theta =63,4\, \textrm{º}##
- Relevant Equations
- ##F=k\Delta x##, ##\sum M_C=0##
Figure:
Attempt at a Solution:
$$F=k\Delta x=lk\sin \theta$$
$$\delta x=0 \quad \textrm{when} \theta=0$$
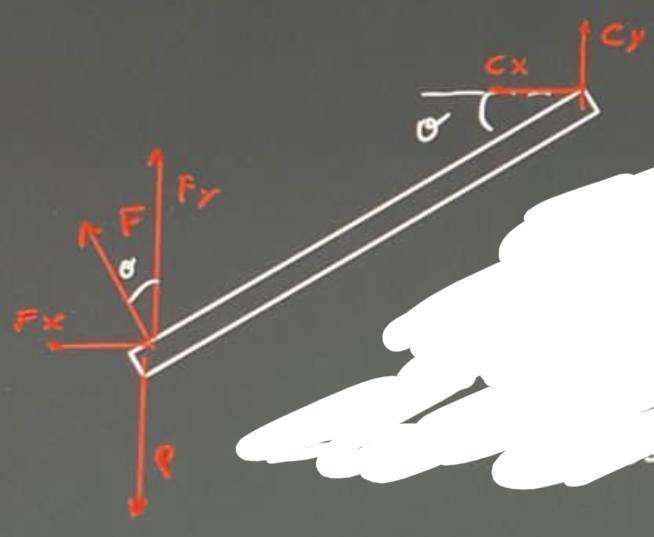
$$\sum M_C=0\rightarrow$$
$$\rightarrow Pl\cos \theta -F_yl\cos \theta -F_xl\sin \theta =0\rightarrow$$
$$\rightarrow Pl\cos \theta -Fl\cos^2 \theta -Fl\sin^2 \theta=0\rightarrow$$
$$\rightarrow Pl\cos \theta -kl^2\sin \theta \cos^2 \theta -kl^2\sin^2 \theta =0\rightarrow$$
$$P\cos \theta =kl\sin \theta \cos^2 \theta -kl\sin^3 \theta =0\rightarrow$$
$$\dfrac{P}{kl}=\dfrac{\sin \theta \cos^2 \theta -\sin^3 \theta}{\cos \theta}\rightarrow \dfrac{P}{kl}=\tan \theta \dfrac{\cos^2 \theta -\sin^2 \theta}{\cos \theta}\rightarrow$$
$$\rightarrow \dfrac{P}{kl}=\dfrac{(\cos \theta +\sin \theta)(\cos \theta -\sin \theta)}{\cos \theta}\tan \theta =(1-\tan^2 \theta)\tan \theta$$
because
$$\left( \dfrac{\cos \theta}{\cos \theta}+\dfrac{\sin \theta}{\cos \theta}\right) \cdot \left( \dfrac{\cos \theta}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}\right) =(1+\tan)\cdot (1-\tan)=$$
$$=1-\tan +\tan -\tan^2 =1-\tan^2 \theta$$
I've tried this but I don't know
Attempt at a Solution:
$$F=k\Delta x=lk\sin \theta$$
$$\delta x=0 \quad \textrm{when} \theta=0$$
$$\sum M_C=0\rightarrow$$
$$\rightarrow Pl\cos \theta -F_yl\cos \theta -F_xl\sin \theta =0\rightarrow$$
$$\rightarrow Pl\cos \theta -Fl\cos^2 \theta -Fl\sin^2 \theta=0\rightarrow$$
$$\rightarrow Pl\cos \theta -kl^2\sin \theta \cos^2 \theta -kl^2\sin^2 \theta =0\rightarrow$$
$$P\cos \theta =kl\sin \theta \cos^2 \theta -kl\sin^3 \theta =0\rightarrow$$
$$\dfrac{P}{kl}=\dfrac{\sin \theta \cos^2 \theta -\sin^3 \theta}{\cos \theta}\rightarrow \dfrac{P}{kl}=\tan \theta \dfrac{\cos^2 \theta -\sin^2 \theta}{\cos \theta}\rightarrow$$
$$\rightarrow \dfrac{P}{kl}=\dfrac{(\cos \theta +\sin \theta)(\cos \theta -\sin \theta)}{\cos \theta}\tan \theta =(1-\tan^2 \theta)\tan \theta$$
because
$$\left( \dfrac{\cos \theta}{\cos \theta}+\dfrac{\sin \theta}{\cos \theta}\right) \cdot \left( \dfrac{\cos \theta}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}\right) =(1+\tan)\cdot (1-\tan)=$$
$$=1-\tan +\tan -\tan^2 =1-\tan^2 \theta$$
I've tried this but I don't know