- #1
torehan
- 41
- 0
In Kronig-Penney Model we seek solutions for time independent Scrödinger equation inside and outside of the periodic potential.
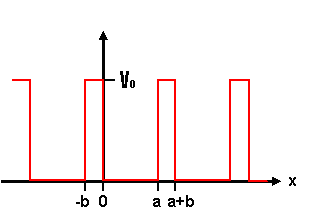
My question is why solution of the KP Scrödinger equation in the region of [tex] -b < x < 0 [/tex] doesnot have complex exponentials as in the region of [tex] 0 < x < a [/tex] ?
for 0 < x < a;
V(x) = V0 for -b < x < 0
My question is why solution of the KP Scrödinger equation in the region of [tex] -b < x < 0 [/tex] doesnot have complex exponentials as in the region of [tex] 0 < x < a [/tex] ?