- #1
Prove It
Gold Member
MHB
- 1,465
- 24
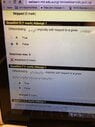
View attachment 5499
To perform implicit differentiation we must make use of the chain rule. Basically if you have a function composed in another function, its derivative is the product of the inner function's derivative and the outer function's derivative. All other rules (such as the sum rule, the product rule, the quotient rule) still apply also.
We must also realize that any combination of "y" functions are essentially a function of x, as y is a function of x. Thus any combination of y's is a composition, and thus must use the chain rule.
For example, $\displaystyle \begin{align*} y^2 \end{align*}$ is composed of an inner function, "y(x)" and an outer function "whatever the output (y) is squared". So the entire function's derivative would be the inner function's derivative, i.e. derivative of y, $\displaystyle \begin{align*} \frac{\mathrm{d}y}{\mathrm{d}x} \end{align*}$ multipled by the outer function's derivative, i.e. derivative of $\displaystyle \begin{align*} y^2 \end{align*}$ which is 2y.
So for the first question:
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x} \, \left( x + y^2 \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x \right) + \frac{\mathrm{d}}{\mathrm{d}x} \, \left( y^2 \right) \\ &= 1 + \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \\ &= 1 + \frac{\mathrm{d}y}{\mathrm{d}x}\,\left( 2\,y \right) \\ &= 1 + 2\,y\,\frac{\mathrm{d}y}{\mathrm{d}x} \end{align*}$
and for the second question:
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^3 + 3\,x\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^3 \right) + 3\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( x\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} \right) \\ &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^3 \right) + 3\,\left[ \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x \right) \, y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^2 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) \right] \\ &= \frac{\mathrm{d}y}{\mathrm{d}x} \,\left( 3\,y^2 \right) + 3 \,\left[ 1 \, y^2 \,\frac{\mathrm{d}y}{\mathrm{d}x} + x \, \frac{\mathrm{d}y}{\mathrm{d}x} \, \frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,\left[ y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,\frac{\mathrm{d}y}{\mathrm{d}x} \, \left( 2\,y \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,\left[ y^2 \,\frac{\mathrm{d}y}{\mathrm{d}x} + 2\,x\,y\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 6\,x\,y\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 + 3\,x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \end{align*}$
To perform implicit differentiation we must make use of the chain rule. Basically if you have a function composed in another function, its derivative is the product of the inner function's derivative and the outer function's derivative. All other rules (such as the sum rule, the product rule, the quotient rule) still apply also.
We must also realize that any combination of "y" functions are essentially a function of x, as y is a function of x. Thus any combination of y's is a composition, and thus must use the chain rule.
For example, $\displaystyle \begin{align*} y^2 \end{align*}$ is composed of an inner function, "y(x)" and an outer function "whatever the output (y) is squared". So the entire function's derivative would be the inner function's derivative, i.e. derivative of y, $\displaystyle \begin{align*} \frac{\mathrm{d}y}{\mathrm{d}x} \end{align*}$ multipled by the outer function's derivative, i.e. derivative of $\displaystyle \begin{align*} y^2 \end{align*}$ which is 2y.
So for the first question:
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x} \, \left( x + y^2 \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x \right) + \frac{\mathrm{d}}{\mathrm{d}x} \, \left( y^2 \right) \\ &= 1 + \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \\ &= 1 + \frac{\mathrm{d}y}{\mathrm{d}x}\,\left( 2\,y \right) \\ &= 1 + 2\,y\,\frac{\mathrm{d}y}{\mathrm{d}x} \end{align*}$
and for the second question:
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^3 + 3\,x\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^3 \right) + 3\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( x\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} \right) \\ &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^3 \right) + 3\,\left[ \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x \right) \, y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^2 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}}{\mathrm{d}x}\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) \right] \\ &= \frac{\mathrm{d}y}{\mathrm{d}x} \,\left( 3\,y^2 \right) + 3 \,\left[ 1 \, y^2 \,\frac{\mathrm{d}y}{\mathrm{d}x} + x \, \frac{\mathrm{d}y}{\mathrm{d}x} \, \frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,\left[ y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,\frac{\mathrm{d}y}{\mathrm{d}x} \, \left( 2\,y \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,\left[ y^2 \,\frac{\mathrm{d}y}{\mathrm{d}x} + 2\,x\,y\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 + x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \right] \\ &= 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 3\,y^2\,\frac{\mathrm{d}y}{\mathrm{d}x} + 6\,x\,y\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 + 3\,x\,y^2\,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} \end{align*}$