- #1
Jdo300
- 554
- 5
Hello all, I'm working on a diagramming program that uses the golden spiral to make templates for something I'm working on. I'm wondering if someone can tell me how to get the equation of the tangent line at point (x,y) on the spiral. My program graphs the spiral parametrically and I use these equations:
X = Cos (T) * Phi ^ ((2 / π) * T)
Y = Sin (T) * Phi ^ ((2 / π) * T)
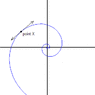
I've uploaded a sample picture to illustrate the spiral graph my program creates. I added a picture of a tangent and a point to show what I'm trying to find. So far, the graphing part of my program works just fine but I'm not quite sure how to do the tangents. I heard that you can use derivatives to do it but I haven't taken Calculus yet so I have no clue how to do them yet. Any help would be greatly appreciated.
Thanks,
Jason O
X = Cos (T) * Phi ^ ((2 / π) * T)
Y = Sin (T) * Phi ^ ((2 / π) * T)
I've uploaded a sample picture to illustrate the spiral graph my program creates. I added a picture of a tangent and a point to show what I'm trying to find. So far, the graphing part of my program works just fine but I'm not quite sure how to do the tangents. I heard that you can use derivatives to do it but I haven't taken Calculus yet so I have no clue how to do them yet. Any help would be greatly appreciated.
Thanks,
Jason O