- #1
FrankJ777
- 140
- 6
- TL;DR Summary
- I'm trying to understand how to take the dot product in spherical coordinates, if that is indeed what I'm supposed to be doing here?
I'm learing about antennas in a course, and we are using Jin's Electromagnetic text.
This isn't a homework problem, I'm just trying to understand what I'm supposed to do in this situation.
This part of the text discusses how to evaluate a radiation pattern.
One of the steps to evaluate the pattern is we have to find an expression for r'cosψ. (See diagram below.)
It says to find the expression, take the dot product between the vector r' and unit vector r.
Like so...[tex]r'⋅ \hat r[/tex]
It gives the formula:
[tex] r' cos ψ = \textbf{r'} ⋅ \hat r = \textbf{r'} ⋅ \hat x cosθsinφ + \textbf{r'} ⋅ \hat y sinθsinφ + \textbf{r'} ⋅ \hat z cosθ [/tex]
I'm confused about what I'm supposed to do, and what I'm supposed to get as an output.
I see that, that expression is the identity for the r component when converting from cartesian to spherical, I'm not sure what's going on.
Am I supposed to convert r' and r_hat to cartesian then take the dot product?
What are the components. [tex]\hat x cosθsinφ [/tex] [tex]\hat y sinθsinφ [/tex] [tex]\hat z cosθ[/tex]
Do I find the θ and φ of r_hat?
I appreciate any help. I'm very confused.
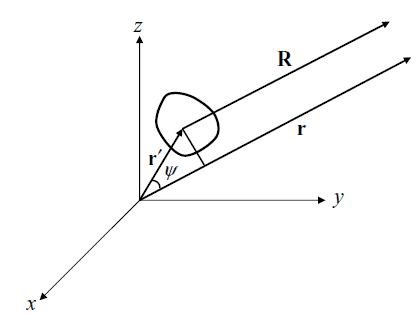
This isn't a homework problem, I'm just trying to understand what I'm supposed to do in this situation.
This part of the text discusses how to evaluate a radiation pattern.
One of the steps to evaluate the pattern is we have to find an expression for r'cosψ. (See diagram below.)
It says to find the expression, take the dot product between the vector r' and unit vector r.
Like so...[tex]r'⋅ \hat r[/tex]
It gives the formula:
[tex] r' cos ψ = \textbf{r'} ⋅ \hat r = \textbf{r'} ⋅ \hat x cosθsinφ + \textbf{r'} ⋅ \hat y sinθsinφ + \textbf{r'} ⋅ \hat z cosθ [/tex]
I'm confused about what I'm supposed to do, and what I'm supposed to get as an output.
I see that, that expression is the identity for the r component when converting from cartesian to spherical, I'm not sure what's going on.
Am I supposed to convert r' and r_hat to cartesian then take the dot product?
What are the components. [tex]\hat x cosθsinφ [/tex] [tex]\hat y sinθsinφ [/tex] [tex]\hat z cosθ[/tex]
Do I find the θ and φ of r_hat?
I appreciate any help. I'm very confused.
Last edited: