- #1
big dream
Problem:
$${\frac {\partial }{\partial t}}A\left( y,t \right) +6\,\Lambda\,\Omega\, \left( {y}^{2}-y \right) \sin \left( t \right) ={\frac {\partial ^{2}}{\partial {y}^{2}}}A \left( y,t \right)$$
$${\frac{\partial }{\partial y}}A \left( t,0 \right) ={\frac {\partial }{\partial y}}A \left( t,1 \right) =0$$
Boundary condition
$${\frac{\partial }{\partial y}}A \left( t,0 \right) ={\frac {\partial }{\partial y}}A \left( t,1 \right) =0$$
ANSWER OF THIS EQUATION IS
$$A \left( y,t \right) =6\,\Lambda\, \left( \Im \right) \, \left\{ [{\frac {i\sinh \left( \alpha\,y \right) }{\alpha}}-{\frac {i \left( 1-\cosh \left( \alpha \right) \right) \cosh \left( \alpha\,y \right) }{\alpha\,\sinh \left( \alpha \right) }}+i{y}^{2}-iy+2\,{\Omega}^{-1}]{{\rm e}^{it}} \right\}$$
Where, $$\alpha=1/2\, \left( 1+i \right) \sqrt {2}\sqrt {\Omega}$$
attempt at a solution
Maple didn't give an answer. I don't know how to get this kind of solution.
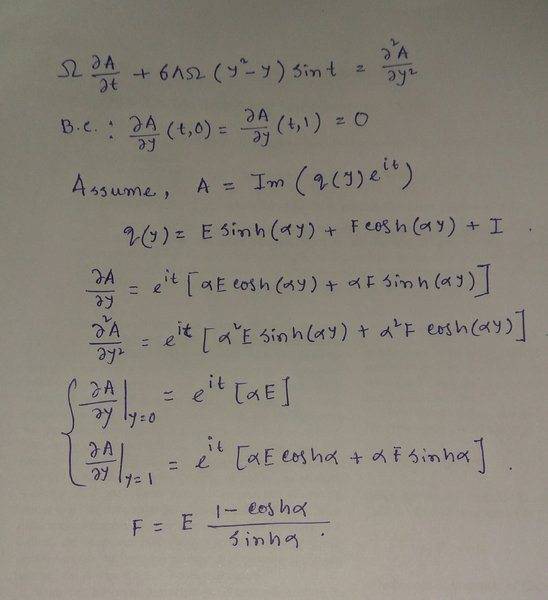
$${\frac {\partial }{\partial t}}A\left( y,t \right) +6\,\Lambda\,\Omega\, \left( {y}^{2}-y \right) \sin \left( t \right) ={\frac {\partial ^{2}}{\partial {y}^{2}}}A \left( y,t \right)$$
$${\frac{\partial }{\partial y}}A \left( t,0 \right) ={\frac {\partial }{\partial y}}A \left( t,1 \right) =0$$
Boundary condition
$${\frac{\partial }{\partial y}}A \left( t,0 \right) ={\frac {\partial }{\partial y}}A \left( t,1 \right) =0$$
ANSWER OF THIS EQUATION IS
$$A \left( y,t \right) =6\,\Lambda\, \left( \Im \right) \, \left\{ [{\frac {i\sinh \left( \alpha\,y \right) }{\alpha}}-{\frac {i \left( 1-\cosh \left( \alpha \right) \right) \cosh \left( \alpha\,y \right) }{\alpha\,\sinh \left( \alpha \right) }}+i{y}^{2}-iy+2\,{\Omega}^{-1}]{{\rm e}^{it}} \right\}$$
Where, $$\alpha=1/2\, \left( 1+i \right) \sqrt {2}\sqrt {\Omega}$$
attempt at a solution
Maple didn't give an answer. I don't know how to get this kind of solution.
