Differential for Real Valued Functions of Several Variables

[Math Amateur]

I am reading the book "Several Real Variables" by Shmuel Kantorovitz ... ...

I am currently focused on Chapter 2: Derivation ... ...

I need help with an aspect of Kantorovitz's Example 3 on pages 65-66 ...

Kantorovitz's Example 3 on pages 65-66 reads as follows:

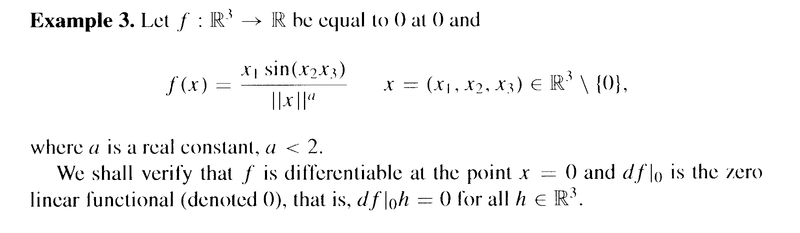
In the above example, we read the following:"... ... ##\frac{ \mid \phi_0 (h) \mid }{ \| h \| } = \frac{ \mid h_1 \text{ sin } (h_2 h_3) \mid }{ \| h \|^{ a + 1 } }## ... ... ... "
My question is as follows:In the Section on The Differential (see scanned text below) ...

Kantorovitz defines ##\phi_x(h)## as follows:

##\phi_x(h) := f(x +h) - f(x) - Lh##

so that

##\phi_0(h) := f(0 +h) - f(0 ) - Lh = f(h) - f(0)## ...... BUT in the Example ... as I understand it ... ##f(0)## does not exist for the function in Example 3 ...? ...

... BUT ... Kantorovitz effectively gives ##\mid \phi_0 (h) \mid = \frac{ \mid h_1 \text{ sin } (h_2 h_3) \mid }{ \| h \| }##
Can someone please explain how Kantorovitz gets this value for ##\mid \phi_0 (h) \mid## when ##f(0)## does not exist?Help will be much appreciated ...

Peter==============================================================================

***NOTE***

Readers of the above post may be helped by having access to Kantorovitz' Section on "The Differential" ... so I am providing the same ... as follows:

Hope that helps in understanding the post ...

Peter

 

[Math Amateur]

I've just noticed that the author defines the function to be zero at zero!

... careless of me to miss that!

My apologies ...

Peter

 

[math771]

Hi Peter,

I can see why you're confused about this example. It does seem like there's a contradiction between Kantorovitz's definition of ##\phi_0(h)## and the fact that ##f(0)## does not exist for the function in Example 3.

However, I believe the key to understanding this lies in the fact that Kantorovitz is using a slightly different definition of the differential for this example. In the section on "The Differential," he defines ##\phi_x(h)## as ##f(x+h) - f(x) - Lh##, as you mentioned.

But in Example 3, he uses a modified version of this definition, specifically for functions that are not differentiable at the point x. He defines ##\phi_x(h)## as ##f(x+h) - f(x)##, rather than ##f(x+h) - f(x) - Lh##. This modified definition allows him to still use the concept of the differential, even for functions that are not differentiable at a point.

So in the example, when he says ##\phi_0(h) := f(0+h) - f(0) - Lh##, he really means ##\phi_0(h) := f(0+h) - f(0)##, which is consistent with his modified definition.

I hope this helps clarify things for you. Let me know if you have any other questions.