- #1
asdf12312
- 199
- 1
can someone confirm i did this rite:
Find I(x)
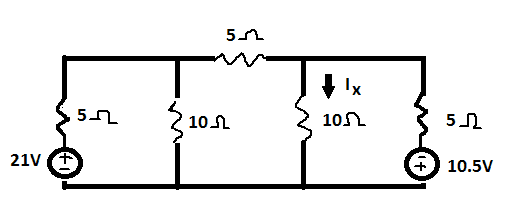
see the next part please
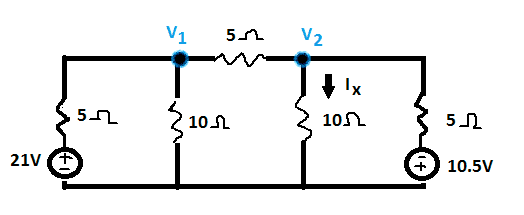
using nodal analysis method i have 2 nodes and these are the equations i got for each, after simplification:
V1: (5/2)V1-V2=21
V2: (5/2)V2-V1=10.5
Using cramer's law, this is matrix i got when i plugged in above equations:
| 5 -2 | |V1| = |42|
| -2 5 | |V2| = |21|
V1=[(42*5)-(21*-2)/(5*5)-(-2*-2)]=12V
V2=[(5*21)-(-2*42)/(5*5)-(-2*-2)]=9V
now recognize that I(x)=V2/10, i got I(x)=0.9A.
so my question is two-part: 1st, did i do this rite? 2nd, is there easier way to solve for I(x)?
Homework Statement
Find I(x)
Homework Equations
see the next part please
The Attempt at a Solution
using nodal analysis method i have 2 nodes and these are the equations i got for each, after simplification:
V1: (5/2)V1-V2=21
V2: (5/2)V2-V1=10.5
Using cramer's law, this is matrix i got when i plugged in above equations:
| 5 -2 | |V1| = |42|
| -2 5 | |V2| = |21|
V1=[(42*5)-(21*-2)/(5*5)-(-2*-2)]=12V
V2=[(5*21)-(-2*42)/(5*5)-(-2*-2)]=9V
now recognize that I(x)=V2/10, i got I(x)=0.9A.
so my question is two-part: 1st, did i do this rite? 2nd, is there easier way to solve for I(x)?