Cylinder on a decelerating truck

[Karol]

Homework Statement

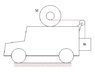
A truck with a cylinder of mass M and moment of inertia ##I=kMR^2## on top has initial velocity v₀ and decelerates with deceleration B. the cylinder is attached with a rope to a weight m. the coefficient of friction is μ.
The outer radius of the cylinder is R and the smaller is r. The cylinder moves without sliding and there isn't friction between the weight m and the truck.
What is the relation between the angular acceleration of the cylinder and the linear acceleration of the weight.
What are the forces and the moments that act on the weight and the cylinder.
What is the linear acceleration of the cylinder in the reference frame of the truck.
What is the condition on B so that the cylinder will move to the right relative to the truck.

Homework Equations

Torque and moment of inertia: ##M=I\ddot{\theta}##

The Attempt at a Solution

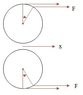
The relation between the accelerations:
$$\frac{\ddot{x}}{r}=\frac{\ddot{y}}{r}=\ddot{\theta}$$
The tension in the rope is T. the forces:
$$\left\{ \begin{array}{l} MBR+Tr=kMR^2\cdot \frac{\ddot{\theta}}{r} \\ mg-T=m\ddot{y} \end{array} \right.$$
$$\rightarrow MBR+m\left( g+\ddot{y} \right)r=kMR^2\cdot \frac{\ddot{\theta}}{r}$$
$$\ddot{y}=\frac{r\left( MBR+mgr \right)}{kMR^2+mr^2}$$
The linear acceleration of the cylinder in reference to the truck:
$$\frac{\ddot{x}}{R}=\ddot{\theta}=\frac{\ddot{y}}{r}=\frac{MBR+mgr}{kMR^2+mr^2}$$
The condition on B:
$$\left\{ \begin{array}{l} mg-T=\ddot{y}m=\ddot{\theta}mR\rightarrow T=m\left( g-R\ddot{\theta} \right) \\ Tr-MBR=kMR^2\cdot \ddot{\theta} \end{array}\right.$$
$$\ddot{\theta}=0 \rightarrow B=\frac{mr}{MR}g$$

 

[haruspex]

For the first part, it is not clear whether the acceleration of the mass is wanted relative to the truck or relative to the vround. Asuuming it's relative to the truck, I believe R should feature in the answer. If the cylinder rotates an angle theta, how far does it move relative to the truck? How far does a horizontal piece of the string move?

 

[Karol]

The relation between the accelerations:
$$\frac{\ddot{y}}{R}=\ddot{\theta}$$
The tension in the rope is T. the forces:
$$\left\{ \begin{array}{l} MBR+Tr=kMR^2\cdot \ddot{\theta} \\ mg-T=m\ddot{y} \end{array} \right.$$
$$\rightarrow MBR+m\left( g+\ddot{y} \right)r=kMR^2\cdot \ddot{\theta}$$
$$\ddot{y}=-\frac{mrg+MBR}{mr-kMR}$$
The linear acceleration of the cylinder in reference to the truck: ##\ddot{x}=\ddot{y}##
The condition on B:
$$\left\{ \begin{array}{l} mg-T=\ddot{y}m=\ddot{\theta}mR\rightarrow T=m\left( g-R\ddot{\theta} \right) \\ Tr-MBR=kMR^2\cdot \ddot{\theta} \end{array}\right.$$
$$\ddot{\theta}=0 \rightarrow B=\frac{mr}{MR}g$$
It comes out also from ##\ddot{y}=0##

 

[haruspex]

The relation between the accelerations: ##\frac{\ddot{y}}{R}=\ddot{\theta}##

No.
Forget the motion of the truck for the moment and consider the cylinder rolling an angle theta, to the right say. The centre of the cylinder has moved ##R\theta## to the right, so the point on the cylinder where the rope first contacts it has also moved ##R\theta## to the right. But there is now more rope wound on the cylinder. How much more? So how far has the rope moved?
Check the answer by considering the extreme cases, r=R, and r=0.

The tension in the rope is T. the forces: ##MBR+Tr=kMR^2\cdot \ddot{\theta}##

That's not right either. Again, let B=0 for the moment. Which way will the cylinder roll? Is the tension in the string the only force exerting a torque on the cylinder?

 

[Karol]

The relation between the accelerations:
$$\ddot{x}=R\ddot{\theta}-r\ddot{\theta}=\ddot{\theta}(R-r)$$
The moment of inertia round the point of contact with roof:
$$I_a=kMR^2+MR^2=MR^2(k+1)$$
The tension in the rope is T. in the frame of the truck d'alambert:

$$\left\{ \begin{array}{l} Tr-MBR=kMR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot{y} \end{array} \right.$$
But i don't know to do it in laboratory frame since the forces are:

And they rotate the cylinder in the same direction, to the left, if i take moments round the center.
And how do i take the sign of ##\ddot{\theta}##? i never knew to do that. do i decide that counterclockwise is positive? but there are two forces, so which one is dominant? if θ rotates in it's direction

 

[haruspex]

##Tr−MBR=kMR^2(k+1)⋅\ddot θ##

I assume the first k on the right is a typo.
How do you get Tr on the left? Isn't this supposed to be the torque the rope generates about the point of contact with the roof?

 

[Karol]

$$T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta}$$
But still how do i solve the forces in the laboratory frame? see the other sketch

 

[haruspex]

$$T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta}$$
But still how do i solve the forces in the laboratory frame? see the other sketch

It's almost the same. You just have to include the truck's acceleration in the total angular acceleration resulting from the torque. I.e. it is a real acceleration instead of a fictitious force. If you have trouble convincing yourself of the validity of this, you can put in a friction force and take moments about the cylinder's centre instead.

 

[Karol]

D'alambert:
$$\left\{ \begin{array}{l} T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m(R-r)\ddot{y} \end{array} \right.$$
$$\rightarrow \ddot{\theta}=\frac{mg(R-r)}{MR^2(k+1)+m(R-r)^2}$$
Laboratory:
$$R\ddot{\theta}=B\rightarrow \ddot{\theta}=\frac{B}{R}$$
$$\left\{ \begin{array}{l} T(R-r)=\left[MR^2(k+1)-\frac{B}{R} \right]\ddot{\theta} \\ mg-T=m(R-r)\ddot{y} \end{array} \right.$$
But i don't get the same result.
It's strange that i made moments round the center for ##R\ddot{\theta}=B## but for T i made moments around the point of contact. is it allowed to combine them into one equation?

 

[haruspex]

Rθ¨=B

How do you get that? Isn't that saying the centre of the cylinder does not accelerate?

 

[Karol]

To simplify suppose there is no rope, only cylinder. if it were a box and the deceleration increases gradually the friction force f would grow until it would reach ##mg\mu##. as long as ##f<mg\mu## the deceleration of the box is B and it stays in place.
If the cylinder was mass-less ##R\ddot{\theta}=B## would be true but with mass the cylinder will rotate slower, but how slow? what's the friction force? if B is big the cylinder will also slide.

 

[haruspex]

If the cylinder was mass-less ##R\ddot{\theta}=B## would be true but with mass the cylinder will rotate slower, but how slow? what's the friction force? if B is big the cylinder will also slide.

Look for a relationship between B, R, r, ##\ddot\theta##, ##\ddot y##.

 

[Karol]

Look for a relationship between B, R, r, ##\ddot\theta##, ##\ddot y##.

I see only kinematics, is it true? no gravitation, Mg?

 

[haruspex]

I see only kinematics, is it true? no gravitation, Mg?

No, sorry, I got that wrong. (Making a lot of mistakes today.)
If you want to take moments about the cylinder's centre then you will need to introduce the force of friction between the cylinder and truck. This contributes both to the rotational acceleration and the linear acceleration in the lab frame. It's the latter that relates to B, R, r, ##\ddot\theta##, ##\ddot y##

 

[Karol]

The acceleration of the center: ##B-R\ddot{\theta}##
Moments round the center:
$$M\left( B-R\ddot{\theta} \right)R+Tr=kMR^2\ddot\theta$$
But the friction f and T act in the same direction, relative to the center and it's not true, B rotates counter clockwise and T clockwise.
If i could take moments round the contact point for T and round the center for f it would be better.

 

[haruspex]

The acceleration of the center: ##B-R\ddot{\theta}##
Moments round the center:
$$M\left( B-R\ddot{\theta} \right)R+Tr=kMR^2\ddot\theta$$
But the friction f and T act in the same direction, relative to the center and it's not true, B rotates counter clockwise and T clockwise.
If i could take moments round the contact point for T and round the center for f it would be better.

I have trouble keeping track of which way positive is being defined for these variables. For the equation in post #7, with which I agree, I believe B is defined as positive to the right and theta as positive clockwise.
On that basis, if a is the linear acceleration of the cylinder's mass centre, to the right, in an inertial frame, ##a = B+R\ddot{\theta}##. If the frictional force on the cylinder is F to the right,
##F+T=Ma=MB+M\ddot\theta R##, ##kMR^2\ddot\theta=-FR-Tr##.
I believe that putting those together leads to the same equation as in post #7.

 

[Karol]

Inertial frame:
$$\left\{ \begin{array}{l} F+T=MB+M\ddot\theta R \\ kMR^2\ddot\theta=-FR-Tr \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
$$\rightarrow \ddot\theta=\frac{mg(R-r)-MRB}{MR^2(k+1)+m(R-r)^2}$$
Truck's frame:
$$\left\{ \begin{array}{l} T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
It gives the same

 

[Karol]

For the equation in post #7, with which I agree, I believe B is defined as positive to the right and theta as positive clockwise.

The equation in post #7 took moments round the contact point so if a force acts to the right θ is positive clockwise. but if i took moments round the center θ would have been positive counter clockwise.
I just want to ask how do i know which way θ is positive, and i assume that for every equation it depends on the pivot point, the axis, right?

 

[haruspex]

The equation in post #7 took moments round the contact point so if a force acts to the right θ is positive clockwise. but if i took moments round the center θ would have been positive counter clockwise.
I just want to ask how do i know which way θ is positive, and i assume that for every equation it depends on the pivot point, the axis, right?

The positive direction for theta, as a variable, is however you choose to define it. You just need to be consistent. The choice is independent of your choices for the linear movements etc.
The value computed for theta may be positive or negative. If you defined it positive clockwise but the value of ##\ddot{\theta}## comes out negative then you know that in fact it rotates counterclockwise.

 

[Karol]

The positive direction for theta, as a variable, is however you choose to define it. You just need to be consistent. The choice is independent of your choices for the linear movements etc.

Doesn't the positive direction of the force define θ?
The equation in post #7:
$$T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta}$$
I could say positive θ is counter clockwise and still the equation would be the same!

 

[haruspex]

Doesn't the positive direction of the force define θ?

It determines which way the angular acceleration, as a value, will be positive, but how you choose to define the variable is up to you.
Consider gravity. It is common to define up as the positive direction. Most people then write that the weight of an object is -mg, g taking a positive value, like 9.8m/s². But it is more logical to say that the weight is mg, and g will take the value -9.8m/s².

I could say positive θ is counter clockwise and still the equation would be the same!

No. If T (as a force on the cylinder) is positive to the right then T(R-r) is a clockwise torque. Similarly MBR represents an anticlockwise torque (because of the way the variables in it are defined), so -MBR is clockwise. If you now want to define θ (and hence ##\ddot\theta##) as anticlockwise then you will need to introduce a minus sign on the right.

 

[Karol]

It determines which way the angular acceleration, as a value, will be positive

How does the direction of the force determine which way is the positive angle?
If you change the point of rotation, if you put the force under or above the point of rotation it changes the direction of torque, like in the drawing.
Or is there another method to decide.

 

[555mr]

**** you bic boi

 

[haruspex]

How does the direction of the force determine which way is the positive angle?
If you change the point of rotation, if you put the force under or above the point of rotation it changes the direction of torque, like in the drawing.
Or is there another method to decide.

Suppose you have defined clockwise as positive and, for linear matters, positive to the right. If a horizontal force F is applied at the top of the circle then the torque is Fr. Check: if the force is in fact to the right then the torque will indeed be clockwise. But note that that we have not actually fixed which way the force F acts. It may be that F has to be deduced from other information. If in reality it acts to the left then its value will be negative. The torque it exerts will then turn out to be negative, i.e. it will in fact be anticlockwise.
If the force F is applied at the bottom then we must write the torque as -Fr.
This comes out a little more naturally in vectors. If the vertical unit vector is j, positive up, then in the top picture the torque is ##r\vec j \times \vec F## (I might have that backwards, but I'll be consistent); in the bottom picture the displacement is ##-r \vec j##.
In short, it is not to do with the directions the forces and torques will turn out to have, it's just a consistent model for representing them.

 

[Karol]

Suppose you have defined clockwise as positive and, for linear matters, positive to the right.

So i can decide independently for F and θ which is the positive direction?
So in the equation from post #7:
$$T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta}$$
How do i know what sign to put on the right term?
Does it have to do with an assumption that i make on the resultant θ?
For example you said that you agree with that formula because θ is positive clockwise. do i have to assume the cylinder will actually turn to the right, or it doesn't have anything to do with the resultant rotation?
Suppose i decide that θ is positive counterclockwise and i assume it will indeed rotate counterclockwise, then the equation will still be the same.

 

[haruspex]

So i can decide independently for F and θ which is the positive direction?

Yes.

How do i know what sign to put on the right term?

Because you have chosen T as positive right, theta as positive clockwise, and R-r is such that an actual positive T would lead to an actual positive angular acceleration.

Does it have to do with an assumption that i make on the resultant θ?

It does not depend on an assumption about how the answer will turn out.

Suppose i decide that θ is positive counterclockwise

An actual T to the right will still lead to an actual clockwise torque, so its effect on theta would then be to reduce it, so you'd need to write -##\ddot\theta##.
The question you have to ask yourself is one of consistency: if T takes a positive value in this equation will the torque be clockwise or counterclockwise? Will the equation give me a positive or negative angular acceleration? Does that match with the sense of the torque?

 

[Karol]

This was the previous result from post #17:
$$\left\{ \begin{array}{l} T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
$$\rightarrow \ddot\theta=\frac{mg(R-r)-MRB}{MR^2(k+1)+m(R-r)^2}$$
Now i change the sign on the right:
$$\left\{ \begin{array}{l} T(R-r)-MBR=-MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
$$\rightarrow \ddot\theta=\frac{MRB-mg(R-r)}{MR^2(k+1)-m(R-r)^2}$$
You see that the value, not only the sign, of ##\ddot\theta## has changed because the denominator is different, i didn't expect that.
So the decision which is the positive direction of the angular displacement changes the value of ##\ddot\theta##? not reasonable

 

[haruspex]

This was the previous result from post #17:
$$\left\{ \begin{array}{l} T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
$$\rightarrow \ddot\theta=\frac{mg(R-r)-MRB}{MR^2(k+1)+m(R-r)^2}$$
Now i change the sign on the right:
$$\left\{ \begin{array}{l} T(R-r)-MBR=-MR^2(k+1)\cdot \ddot{\theta} \\ mg-T=m\ddot\theta (R-r) \end{array} \right.$$
$$\rightarrow \ddot\theta=\frac{MRB-mg(R-r)}{MR^2(k+1)-m(R-r)^2}$$
You see that the value, not only the sign, of ##\ddot\theta## has changed because the denominator is different, i didn't expect that.
So the decision which is the positive direction of the angular displacement changes the value of ##\ddot\theta##? not reasonable

If you change the direction in which the angle is measured then all occurrences of ##\ddot \theta## in the equations must flip sign.

 

[Karol]

Because you have chosen T as positive right, theta as positive clockwise, and R-r is such that an actual positive T would lead to an actual positive angular acceleration.

An actual T to the right will still lead to an actual clockwise torque, so its effect on theta would then be to reduce it, so you'd need to write -##\ddot\theta##.

You mean to say that i have to consider the whole torque side, the left side of:
$$M=I\ddot\theta\rightarrow T(R-r)-MBR=MR^2(k+1)\cdot \ddot{\theta}$$
I have to consider not only if T gets a positive value, because there is also the term -MBR

The question you have to ask yourself is one of consistency: if T takes a positive value in this equation will the torque be clockwise or counterclockwise? Will the equation give me a positive or negative angular acceleration? Does that match with the sense of the torque?

So if the system, in this case the cylinder, actually yields to the torque and rotates in the same direction of the torque, that is what i have to consider, right? and by that direction to decide, in accordance with the positive direction of θ that i have decided upon, which is the sigh of the right side of the equation ##M=I\ddot\theta##, the ##I\ddot\theta## side?

 

[Karol]

What is the condition on B that the cylinder will rotate right relative to the truck?
$$\ddot\theta=\frac{mg(R-r)-MRB}{MR^2(k+1)+m(R-r)^2}$$
$$\ddot\theta>0\rightarrow mg(R-r)-MRB>0 \rightarrow B<\frac{mg(R-r)}{MR}$$