- #1
sirfederation
- 20
- 0
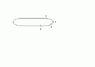
Here we are looking down on a racetrack with straight sections and semicircular ends. A car is going around the track and maintaining constant speed.
For each one of the numbered positions: Draw diagrams showing the velocity vector for the car.
I will post my diagrams on a separate reply. I just need to know if I am getting this concept down (this is yet another example concept from the book I am not getting). My question is do I have a total of three diagrams. One would be for #1 as Vi and #2 as Vf. Then the second diagram starts with #2 as Vi and #3 as Vf. The third diagram as #3 as Vi and #4 as Vf. I should have a reply with my diagrams on it
For each one of the numbered positions: Draw diagrams showing the velocity vector for the car.
I will post my diagrams on a separate reply. I just need to know if I am getting this concept down (this is yet another example concept from the book I am not getting). My question is do I have a total of three diagrams. One would be for #1 as Vi and #2 as Vf. Then the second diagram starts with #2 as Vi and #3 as Vf. The third diagram as #3 as Vi and #4 as Vf. I should have a reply with my diagrams on it