- #1
noob314
- 18
- 0
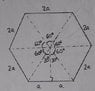
A plastic rod with a total charge Q uniformly distributed along its length is bent into a regular hexagon where each side has a length of 2a, as shown below. Calculate the electric potential at the center of the hexagon (relative to the point at infinity).
I wasn't sure how to exactly start this problem, so what I did was "simplify" the hexagon into 6 points with a charge of Q/6 on each end of the hexagon and calculated the electric potential of each point from the equation V = kQ/r, giving the total potential of kQ/2a at the center. I'm not sure if that's the correct way to go about in solving this problem, as I don't know the final answer, so any help is appreciated. Thanks.
I wasn't sure how to exactly start this problem, so what I did was "simplify" the hexagon into 6 points with a charge of Q/6 on each end of the hexagon and calculated the electric potential of each point from the equation V = kQ/r, giving the total potential of kQ/2a at the center. I'm not sure if that's the correct way to go about in solving this problem, as I don't know the final answer, so any help is appreciated. Thanks.