BRS: Penrose-Carter Conformal Compactifcations of Spacetimes

[Chris Hillman]

I. Overview

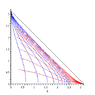
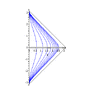
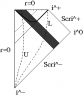
Penrose-Carter diagrams are one of the most useful techniques for visualizing the global causal structure of a Lorentzian manifold. Their most distinctive features are

• such a diagram is actually a conformal coordinate chart, so (with angular dimension suppressed, to make a two-dimensional diagram) lines with slope +/-1 represent null geodesics,
• the domain of the chart includes the entire manifold (or almost all of it), so it is a global chart (or very nearly so),
• the domain is compact, so important geometric loci such as
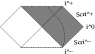
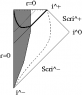
  • "the sphere at spatial infinity"
  • future lightlike infinity
  are clearly represented within a bounded region

For all these reasons, Penrose diagrams clearly reveal how a spacetime typically consists of various regions which are related to each other in ways which are clearly revealed in the diagram, but hard to appreciate by other means. In particular, we may see that observers in region A can send signals to observers in region B, but not vice versa.

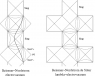
Penrose diagrams are most often drawn for spacetimes which happen to be spherically symmetric, and are often drawn with the angular coordinates suppressed to make a two-dimensional diagram. But they can be constructed for cylindrical and planar symmetry and are equally valuable in those situations. In all cases, Penrose diagrams are generally the best way to immediately grasp the nature of global Killing flows (for example, how the global flow associated with "time translation" in the exterior of a black hole may appear as a spatial translation in an interior region).

In the spherically symmetric case, Penrose diagrams clearly reveal physically important characteristics of the principle null geodesic congruences. And by studying Penrose diagrams of simple spherically symmetric gravitational collapse models we can gain valuabl e insight into such essential but subtle concepts as

• event horizons, their "teleological" nature, and the standard definition of "black hole",
• apparent horizons
• Cauchy horizons
• various types of cosmological horizons
• wormholes of various types

More technical virtues--- whose value becomes apparently only after further explanation--- include the fact that one can integrate over a region of "future lightlike infinity" to compute such interesting quantities as the mass-energy lost from a dynamic isolated gravitating system due to gravitational radiation.

A little appreciated virtue is that Penrose diagrams are also very useful for understanding the relationship between various different classes of observers in a given spacetime model.

In this thread I plan to

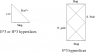
• provide a fairly detailed introduction to the Penrose diagram for Minkowski vacuum, with figures, including a discussion of how to "read" a typical Penrose diagram,
• a more sketchy, but illustrated, introduction to Penrose diagrams for various familiar black hole models: Schwarzschild vacuum, Reissner-Nordstrom electrovacuum, de Sitter lambdavacuum, Kerr vacuum,
• a sketchy illustrated survey of Penrose diagrams for related solutions, including Taub-NUT vacuum, Vaidya models, Maeda wormhole, (perhaps) some CPW models of gravitational collapse,
• a sketchy illustrated survey of Penrose diagrams for some cosmological models, including FRW dusts, the horizon problem, FRW radiation fluids, LTB dusts, Mcvittie spherically symmetric perfect fluid, Senovilla-Vera dust
• a sketchy survey of the Levi-Civita type AIII Petrov D vacuum (E^2 symmetric Kasner vs. Taub planar symmetric vacuum), the Levi-Civita type C Petrov D vacuum and (perhaps) a related solution, the Bonnor-Swaminarayan vacuum, plus transversable wormholes.

I anticipate that most of the work will consist of preparing the figures!

My hope is that SA/Ms will painlessly become sufficiently familiar with the uses of Penrose diagrams to make their own and use them in threads in the public areas. With some figures and a bit of handholding, I think at least some readers in the public areas will be able to appreciate that these diagrams are a very efficient way of conveying information.

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. II. Minkowski Vacuum

Start with the usual polar spherical chart for Minkowski vacuum
[tex]
ds^2 = -dt^2 + dr^2 + r^2 \, d\Omega^2
[/tex]
where [itex]d\Omega^2 = d\theta^2 + \sin(\theta)^2 \, d\phi^2[/itex] is the line element of a unit sphere in polar spherical coordinates. Constructing a conformally compactified chart for Minkowski vacuum is straightforward once you know the basic trick: first transform to a double null chart
[tex]
u = t-r, \; \; v = t+r
[/tex]
which gives
[tex]
ds^2 = -du \, dv + \frac{(v-u)^2}{4} \; d\Omega^2
[/tex]
Next, we compactify
[tex]
p = \arctan(u), \; q = \arctan(v)
[/tex]
which gives
[tex]
ds^2 = \frac{-dp \, dq}{\cos(p)^2 \, \cos(q)^2} + \frac{ \sin(q-p)^2/4}{\cos(p)^2 \, \cos(q)^2} \; d\Omega^2
[/tex]
Finally,
[tex]
T = q+p, \; \; R = q-p
[/tex]
gives (after some elementary trigonometric manipulations)
[tex]
\begin{array}{rcl}
ds^2 & = & \frac{1}{(\cos(T) + \cos(R))^2} \; \left[ -dT^2 + dR^2 + \sin(R)^2 \, d\Omega^2 \right], \\
&& -\pi < T < \pi, \; 0 < R < |T|
\end{array}
[/tex]
This line element shows that the Minkowski metric is related by a conformal scale factor to the metric of the Einstein static lambda-dust. We'll call the resulting coordinate chart (which turns out to be almost global--- it omits the locus R=0, so strictly speaking it is not quite a global chart, although that is easily remedied by introducing "pseudocartesian" coordinates) the Penrose chart.

Unraveling the sequence of coordinate transformations, we find that the transformation from the polar spherical chart to the Penrose chart is
[tex]
T = \arctan(t+r) + \arctan(t-r), \; \; R = \arctan(t+r) - \arctan(t-r)
[/tex]
The inverse transformation may be written (after some more elementary trigonometric manipulations):
[tex]
t = \frac{\sin(R)}{\cos(R)+\cos(T)}, \; \; r = \frac{\sin(T)}{\cos(R)+\cos(T)}
[/tex]
Using the latter we can immediately plot contours [itex]r=r_0[/itex] in the Penrose chart; these will correspond to the world lines of static observers. Also, we can plot contours [itex]t=t_0[/itex], which will correspond to the unique family of orthogonal hyperslices (each is of course isometric to E^3). Usually we suppress the angular coordinates, so that we plot curves in a diamond shaped region, and interpret these as respectively the world sheets of concentric spheres of static observers, and (quotients of) the family of orthogonal hyperslices. See the figure below and note that
[tex]
\frac{\sin(R)}{\cos(R)+\cos(T)} = r_0
[/tex]
gives
[tex]
T = \pi - \arccos( \cos(R) - \sin(R)/r_0)
[/tex]
which covers the top half of the contours shown in blue, and so on.

Notice that the volume form is
[tex]
\frac{\sin(R)^2}{(\cos(T)+\cos(R))^2} \; \sin(\Theta) \; dT \wedge dR \wedge d\Theta \wedge d\Phi
= r^2 \; \sin(\theta) \; dt \wedge dr \wedge d\theta \wedge d\phi
[/tex]

Because the line element we found for our Penrose chart is diagonal, we can immediately read off a frame field
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & ( \cos(T) + \cos(R) ) \; \partial_T \\
\vec{e}_2 & = & ( \cos(T) + \cos(R) ) \; \partial_R \\
\vec{e}_3 & = & ( \cos(T) + \cos(R) ) \; \frac{1}{R} \; \partial_\theta \\
\vec{e}_4 & = & ( \cos(T) + \cos(R)) \[ \frac{1}{R \, \sin(\theta))} \; \partial_\phi
\end{array}
[/tex]
This is nonspinning non-inertial frame field; it corresponds to a family of observers each of which has constant acceleration, but this timelike congruence is quite different from the Rindler congruence. We'll refer to the corresponding family of observers as the Penrose observers.

Specifically, the acceleration vector is
[tex]
\nabla_{\vec{e}_1} \vec{e}_1 = \sin(R) \; \vec{e}_2
[/tex]
Thus, the Penrose observer with world line [itex]R=R_0, \; \theta=\theta_0, \; \phi=\phi_0 [/itex] has constant acceleration, as promised. (Note that the central observer, the one at R=0, is distinguished by having vanishing acceleration, i.e. this one Penrose observer is in a state of inertial motion throughout.) The expansion tensor (components taken wrt the frame field) of our timelike congruence shows homogeneous contraction followed by expansion:
[tex]
{H\left[\vec{e}_1\right]}_{ab} = \sin(T) \; \operatorname{diag} (1,1,1)
[/tex]
The vorticity vanishes, so this is an irrotational congruence, admitting a unique family of orthogonal hyperslices, which is of course the family [itex]T=T_0[/itex]. These have uniform curvature [itex]-\sin(T)^2[/itex], so they are each isometric to [itex]H^3[/itex], with curvature which decreases to a minimum at T=0 and then increases again.

Using our coordinate transformation we can transform the given expressions for the frame vector fields back into the polar spherical chart, finding
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & \frac{1+t^2+r^2}{ \sqrt{1+(t+r)^2} \, \sqrt{1+(t-r)^2} } \; \partial_t
+ \frac{2 \, tr}{ \sqrt{1+(t+r)^2} \, \sqrt{1+(t-r)^2} } \; \partial_r \\
\vec{e}_2 & = & \frac{2 \, tr}{ \sqrt{1+(t+r)^2} \, \sqrt{1+(t-r)^2} } \; \partial_t
+ \frac{1+t^2+r^2}{ \sqrt{1+(t+r)^2} \, \sqrt{1+(t-r)^2} } \; \partial_r \\
\vec{e}_3 & = & \frac{1}{r} \; \partial_\theta \\
\vec{e}_4 & = & \frac{1}{r \, \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
For comparision, the Milne frame (written in the polar spherical chart) is
[tex]
\begin{array}{rcl}
\vec{f}_1 & = & \frac{1}{\sqrt{t^2-r^2}} \; \left( t \, \partial_t + r \, \partial_r \right) \\
\vec{f}_2 & = & \frac{1}{\sqrt{t^2-r^2}} \; \left( r \, \partial_t + t \, \partial_r \right) \\
\vec{f}_3 & = & \frac{1}{r} \; \partial_\theta \\
\vec{f}_4 & = & \frac{1}{r \, \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
Recall that the Milne congruence consists of the world lines of a family of inertial observers who exhibit homogeneous contraction, passing through a common event (where the congruence is briefly singular) and then re-expanding, with homogeneous expansion, making a "Poor Man's cosmological model", in the phrase of J. A. Wheeler. We can transform these frame vectors to represent them explicitly in the Penrose chart, but to draw the world lines of the Milne observers in the Penrose chart, it is easier to notice that they are given by [itex]t/r = k[/itex], from which we find the corresponding characterization in terms of the Penrose coordinates (see figure).

Comparing the figures illustrating the world lines of static and Milne observers, we note that all of them end at a certain point on the boundary of the Penrose diagram, the point conventionally labeled [itex]i^+[/itex], called future timelike infinity. This is no coincidence: these are all the world lines of inertial observers, i.e. they are timelike geodesics, and it turns out that all such paths terminate in [itex]i^+[/itex].

A timelike congruence which is is obviously closely related to the Milne congruence, but which consists of non-geodesic timelike curves (i.e., the world lines of certain accelerating observers) is associated with a third frame field, which can be written in the polar spherical chart like this:
[tex]
\begin{array}{rcl}
\vec{g}_1 & = & \frac{1}{\sqrt{t^2-r^2}} \; \left( r \, \partial_t + t \, \partial_r \right) \\
\vec{g}_2 & = & \frac{1}{\sqrt{t^2-r^2}} \; \left( t \, \partial_t + r \, \partial_r \right) \\
\vec{g}_3 & = & \frac{1}{r} \; \partial_\theta \\
\vec{g}_4 & = & \frac{1}{r \, \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
This is a version of the Rindler frame, in which each observer is accelerating with constant magnitude proportional to distance from the origin, so that the world lines are arranged in a spherically symmetric fashion instead of a plane symmetric fashion. (This allows us to suppress the inessential angular coordinates when studying the situation in the Penrose chart.) The acceleration vector is
[tex]
\nabla_{\vec{g}_1} \vec{g}_1 = \frac{1}{\sqrt{r^2-t^2}} \; \vec{g}_1
[/tex]
(Note that the world lines obtained as the integral curves of [itex]\vec{g}_)1[/itex] are hyperbolas, so the magnitude and direction of acceleration is constant for each of our observers.) The expansion tensor (components taken wrt the given frame field!) is
[tex]
{H\left[\vec{g}_1\right]}_{ab} = \frac{t/r}{\sqrt{r^2-t^2}} \; \operatorname{diag}(0,1,1)
[/tex]
which shows in particular that [itex]H_{22} = 0[/itex], so neighboring observers who are radially separated maintain constant distance from each other. The vorticity vector vanishes, so the congruence is hypersurface orthogonal, and the unique family of orthogonal hyperslices has three-dimensional Riemann tensor
[tex]
r_{3434} = \frac{-t^2/r^2}{r^2-t^2}
[/tex]
so each slices has geometry like [itex]\mathbb{R} \times H^2[/itex] but with the Gaussian curvature of the H^2 factor varying with r.

We can transform our frame field to represent it in the Penrose chart:
[tex]
\begin{array}{rcl}
\vec{g}_1 & = & \sqrt{\frac{\cos(T)+\cos(R)}{\cos(T)-\cos(R)}} \; \left( \cos(T) \, \sin(R) \, \partial_T + \sin(T) \, \cos(R) \, \partial_R \right) \\
\vec{g}_2 & = & \sqrt{\frac{\cos(T)+\cos(R)}{\cos(T)-\cos(R)}} \; \left( \sin(T) \, \cos(R) \, \partial_T + \cos(T) \, \sin(R) \, \partial_R \right) \\
\vec{g}_3 & = & \frac{\cos(T)+\cos(R)}{\sin(R)} \; \partial_\theta \\
\vec{g}_4 & = & \frac{\cos(T)+\cos(R)}{\sin(R)} \; \frac{1}{\sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
In terms of the Penrose chart, we have
[tex]
\begin{array}{rcl}
\nabla_{\vec{g}_1} \vec{g}_1 & = & \sqrt{\frac{\cos(T)+\cos(R)}{\cos(T)-\cos(R)}} \; \vec{g}_1 \\
& = & \frac{1}{\sqrt{r^2-t^2}} \; \vec{g}_1
\end{array}
[/tex]
We know that the magnitude of this vector is constant for each observer, i.e. it happens to be an invariant of the motion, so from
[tex]
\frac{\cos(T)+\cos(R)}{\cos(T)-\cos(R)} = k^2
[/tex]
we obtain
[tex]
T = \arccos \left( \frac{k^2+1}{k^2-1} \; \cos(R) \right)
[/tex]
as the equation of the world lines in the Penrose chart (see the figures below). This time, we see that the world lines do all end up at the same point on the boundary of the Penrose diagram, but not [itex]i^+[/itex].

For completeness, the static frame is simply
[tex]
\begin{array}{rcl}
\vec{h}_1 & = & \partial_t = (1+\cos(T) \, \cos(R)) \, \partial_T - \sin(T) \, \sin(R) \, \partial_R \\
\vec{h}_2 & = & \partial_r = -\sin(T) \, \sin(R) \, \partial_T + (1 + \cos(T) \, \cos(R)) \, \partial_R \\
\vec{h}_3 & = & \frac{1}{r} \; \partial_\theta = \frac{\cos(T)+\cos(R)}{\sin(R)} \, \partial_\theta \\
\vec{h}_4 & = & \frac{1}{r \, \sin(\theta)} \; \partial_\phi = \frac{\cos(T)+\cos(R)}{\sin(R)} \; \frac{1}{\sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
where we immediately transform the frame vector fields (recall these are simply unit vector fields, which can be transformed according to the usual rules to write them in any local coordinate chart) to obtain the representation of the frame in the Penrose chart.

FIgures: left to right

• contours [itex]r=r_0[/itex] (blue) and [itex]t=t_0[/itex] (red) in the region [itex]0 < T < \pi, 0 < R < T[/itex]; the red and blue curves are everywhere orthogonal to each other wrt the given Lorentzian metric,
• conventional labeling of loci in the Penrose diagram; the entire manifold corresponds to the interior of the "triangle",
• typical world lines of four classes of observers (sketch).

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. II. Minkowski Vacuum cont'd

(cont'd)

Figures: Some world lines (blue) of certain observers in Minkowski vacuum, drawn in the Penrose chart. Left to right:

• static observers (inertial)
• (expanding) Milne observers (inertial)
• (spherically symmetric configuration of) Rindler observers (noninertial)

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. II. Minkowski Vacuum cont'd

(cont'd)

Perhaps the most important aspect of a Penrose diagram (for a spherically symmetric spacetime) is that it allows us to analyze the global characteristics of the principle null geodesic congruences.

Returning to the original chart,
[tex]
ds^2 = -dt^2 + dr^2 + r^2 \, d\Omega^2
[/tex]
the principle outgoing null geodesic congruence is given by the null vector field
[tex]
\vec{k} = \partial_t + \partial_r = (1 + \cos(T+R)) \; \left( \partial_T + \partial_R \right)
[/tex]
where we immediately transform this vector field to obtain its representation in the Penrose chart. This null geodesic congruence has optical scalars
[tex]
\theta\left[\vec{k}\right] = \frac{1}{r} = \frac{\cos(T)+\cos(R)}{\sin(R)},
\; \; \sigma\left[\vec{k}\right] = \omega\left[\vec{k}\right] = 0
[/tex]
which shows the pattern diagnostic of a spherically expanding null geodesic congruence. (There is an unfortunate notational conflict between the coordinate [itex]\theta[/itex] and the standard notation for the optical expansion scalar, which will hopefully not cause confusion, especially since we have added the null geodesic congruence we intend in brackets.) We should think of this congruence as being associated with concentric spherical wavefronts which expand from r=0 (equivalently, from R=0). In the Penrose diagram (with the angular coordinates suppressed), the world sheet of an expanding spherical wavefront appears as a diagonal line segment with slope dR/dT=1.

Similarly, the principle ingoing null geodesic congruence is given by
[tex]
\vec{\ell} = \partial_t - \partial_r
[/tex]
where I leave it as an exercise to transform this vector field to obtain its representation in the Penrose chart. This null geodesic congruence has optical scalars
[tex]
\theta\left[\vec{\ell}\right] = - \, \frac{1}{r} = - \, \frac{\cos(T)+\cos(R)}{\sin(R)},
\; \; \sigma\left[\vec{\ell}\right] = \omega\left[\vec{\ell}\right] = 0
[/tex]

For practice, contemplate the figure below, where I have sketched

• the world sheet (dashed) of a (static) sphere of static observers, near the center of spherical symmetry r=0
• the world sheet (dashed) of a (initially contracting, then expanding) sphere of accelerating observer; this sphere always remains concentric with but outside the first sphere,
• the world sheet (dotted) of an expanding spherical wavefront (diagonal segment with slope dR/dT=1); as you follow this world sheet from lower left rightwards and upwards, the sphere (represented as a point moving along the segment) expands in surface area,
• the world sheet (dotted) of contracting spherical wavefront (diagonal segment with slope dR/dT = -1), which intersects the expanding wavefronts in the world sheet of our sphere of accelerating observers.

Try to mentally superimpose on this diagram the contours of the coordinate r (recall that a coordinate is simply a monotonic function on our spacetime) and to verify that the informal description I offered is fully consistent with these contours. You can rotate the figure I drew about R=0 to restore one of the angular variables. Notice that the family of horizontal circles centered at R=0 gives the trajectories of the Killing flow associated with axial symmetry, while the world lines of the static observers gives the Killing flow associated with "time translation". Next, you can mentally replace horizontal circles with two dimensional spheres.

Such a figure might occur, for example, in a discussion of how a static observer might define and measure the "radar distance" to a distant accelerating observer, by emitting radar pips which are reflected by the moving target, and dividing by two their round trip travel time. This is one of many operationally significant notions of "distance in the large" which can be used to obtain competing notions of "distance in the large". All of them agree for small distances but can differ considerably at large distances. Ignoramuses often mistake misconceptions involving this point as alleged evidence that (they believe) "gtr fails at large distances" [sic].

Returning to the derivation of the Penrose chart in Post #1, I said we can compactify our coordinates using the arctan function. You might well suspect that there are many alternative choices! We do in fact have considerable freedom in constructing Penrose diagrams (i.e. alternative conformal compactifications), but as usual it makes sense to make a simple choice. See the figure below; I'll leave it as an exercise to decide which functions work (recall that the domain of our chart should be compact, and the chart should also be conformal; that's all we need).

To avoid possible confusion, I should probably mention that there are many "Penrose diagrams" used in physics. In gtr, the other two most often seen are a diagram illustrating the relationship between the various Petrov types (in the classification of the possible algebraic symmetries of the Weyl curvature tensor) and Penrose's diagrammatric notation for "index gymnastics" (extensively employed in his recent book The Road to Reality and in many of his other writings). The notion of conformal compactification is quite natural from the viewpoint of algebraic geometry, and it is no accident that this notion was introduced into classical gravitation by Roger Penrose, a mathematician whose graduate training was in algebraic geometry. This was a suitable field for him, since he thinks visually and has proven to be a prolific inventor of amusing pictorial puzzles. Between me and the SA/Ms, I once had the unique pleasure of showing him an amusing picture which connects two of his interests, Penrose tilings and spacetime diagrams. Take a Penrose tiling by fat and thin rhombuses, and interpret each rhombus as a distorted square. Interpret each line segments with slope +/-1 in each square (corrected for the distortion) as a null geodesic segment. Knit the tiling with vertices removed into a locally flat Lorentzian manifold in the now obvious manner. Then, we can regard this as "combinatorial model" of a Lorentzian manifold (two dimensional "spacetime") with curvature concentrated in the vertices. Now, the null geodesics have a surprisingly complicated character. If you find a picture of a Penrose tiling by fat and thin rhombs and try out this construction, you'll find a variety of closed curves which are related to (but distinct from) certain closed curves introduced by J. H. Conway. This gives a kind of combinatorial dynamics on Penrose tilings; some of you may wish to look for the requisite notion of combinatorial Hamiltonian.

Figures: left to right:

• a simple scenario depicted in the Penrose diagram for the Minkowski vacuum,
• Penrose's "compatification function" and a proposed alternative (integrate the "Poor Man's Bell curves" [itex]1/(1+u^2), \; 1/(1+u^2)^2/2[/itex] respectively); both functions map the real line onto a bounded interval.

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. III. Schwarzschild vacuum

The Penrose diagram for the Schwarzschild vacuum is very well known, but I'll review it here anyway.

Recall that we can obtain the Schwarzschild vacuum very naturally by considering a spherically symmetric infalling frame
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & \partial_\tau - f \; \partial_r \\
\vec{e}_2 & = & \partial_r \\
\vec{e}_3 & = & \frac{1}{r} \; \partial_\theta \\
\vec{e}_4 & = & \frac{1}{r \, \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
where f is an undetermined function of [itex]\tau, r[/itex] only. The demanding that the Einstein tensor forces f to be a function of r only, in fact after choosing a real parameter m we must have [itex] f = \sqrt{2m/r}[/itex], which gives the Schwarzschild vacuum in the ingoing Painleve chart, with line element
[tex]
\begin{array}{rcl}
ds^2 & = & -(1-2m/r) \; d\tau^2 - 2 \; \sqrt{2m/r} \; d\tau \; dr + dr^2 + r^2 \; d\Omega^2, \\
&& -\infty < \tau < \infty, \; 0 < r < \infty, \\
&& d\Omega^2 = d\theta^2 +\sin(\theta)^2 \; d\phi^2
\end{array}
[/tex]
We see from the form of the timelike unit vector field [itex]\vec{e}_1[/itex] that differences in the Painleve time coordinate \tau measured along an integral curve of [itex]\vec{e}_1[/itex] (a timelike geodesic) give the elapsed proper time measured by the observer with that world line. This defines the Lemaitre congruence, the timelike geodesic congruence consisting of the world lines of inertial observers who "fall from rest at r=\infty" into our static black hole.

The radial coordinate r has an obvious geometric interpretation in terms of the surface area of the spheres [itex]r=r_0[/itex], and also in terms of the uniform Gaussian curvature [itex]1/r_0^2[/itex] of the spheres [itex]r=r_0[/itex] (we'll see that it has an even more important physical interpretation). but differences in r do not correspond to proper length along radial geodesics [itex]t=t_0, \; \theta=\theta_0, \; \phi=\phi_0[/itex]. The Kretschmann scalar (a quadratic curvature invariant) is
[tex]
R_{abcd} \, R^{abcd} = \frac{48 m^2}{r^6}
[/tex]
which unambiguously shows that the locus r=0 is a spacelike curvature singularity (in fact, a strong singularity in the sense of Ellis and Schmidt., since it crushes and destroys falling bodies as they proceed into their future).

Solving the Killing equations for the ingoing Painleve line element, we find a four dimensional Lie algebra of Killing vector fields:

• [itex]\partial_\tau[/itex], which is
  • timelike irrotational on [itex] 2m < r < \infty[/itex], so the spacetime is static spherically symmetric on this region,
  • null on r = 2m (part of the event horizon, as it will turn out),
  • spacelike noncyclic on [itex] 0 < r < 2m[/itex], so the spacetime is dynamic and admits (contracting) [itex]\mathbb{R} \times S^2[/itex] hyperslices on this region,
• [itex]\partial_\phi[/itex], which is spacelike cyclic (axial rotation of the nested spheres [itex]r=r_0[/itex])
• the other two Killing vectors associated with the action of SO(3) on the system of nested spheres

The static exterior region [itex]2m < r < \infty[/itex] is asymptotically flat, so we can compute the Komar integrals, finding that the Komar mass is m and the Komar spin vanishes. Thus, we have an model of an isolated nonspinning massive object of mass m. The Komar integrals are independent of coordinates, so this justifies our choice for the "mass parameter" m above. Alternatively, computing the electroriemann tensor (tidal tensor) wrt the Lemaitre frame shows the Coulomb form [itex]m/r^3 \; \operatorname{diag}(-2,1,1)[/itex]. This shows again that r=0 represents a strong curvature singularity, but the locus r=2m is locally "no place special".

We can find new coordinates in the exterior region in which the line element is diagonalized; this of course leads to the familiar chart introduced by Schwarzschild 1916, which is related to the ingoing Painleve chart by
[tex]
t= \tau - \int \frac{\sqrt{2m/r}}{1-2m/r} \, dr
[/tex]
In the Schwarzschild chart, it is clear that the exterior region is symmetric under a discrete symmetry, time reversal, so we must have an outgoing Painleve chart whose domain overlaps with the ingoing Painleve chart in the exterior region; it is given by
[tex]
t= \tilde{\tau} + \int \frac{\sqrt{2m/r}}{1-2m/r} \, dr
[/tex]
Thus, we have in addition to the exterior region at least two further regions, future interior and past interior. (You can peek at a figure in Post #6 below for depictions of several regions in the Penrose chart for the Schwarzschild vacuum, which at this point we have not constructed--- but it probably helps to know where we are going with this discussion!).

The interior region is non-static, and we can diagonalize it to find what is sometimes called the "interior Schwarzschild chart" in which the new time coordinate vector [itex]\partial_\bar{t}[/itex] turns out to give a timelike geodesic congruence, which defines the (future part of the) world lines of the so-called Frolov observers. The exterior and interior Schwarzschild charts are adapted to the Killing flow, so they have a simple appearance, but their domains are non-overlapping, so they are useless for understanding how the exterior and future interior regions are related.

Returning to the ingoing Painleve chart, we find three null geodesic congruences:

• a contracting congruence defined on the exterior and future interior regions:
  [tex]
  \vec{k}_1 = \frac{1}{1+\sqrt{2m/r}} \; \partial_\tau - \partial_r
  [/tex]
  which has optical expansion scalar -1/r and vanishing shear and twist scalars,
• a expanding congruence defined on the exterior region (and extensible into the past interior region if we switch to the outgoing Painleve chart)
  [tex]
  \vec{k}_2 = \frac{1}{1-\sqrt{2m/r}} \; \partial_\tau + \partial_r
  [/tex]
  which has optical expansion scalar 1/r and vanishing shear and twist scalars
• (part of) a contracting congruence defined in the interior region (and extensible into a new exterior region)
  [tex]
  \vec{k}_3 = \frac{1}{\sqrt{2m/r}-1} \; \partial_\tau - \partial_r
  [/tex]
  which has optical expansion scalar -1/r and vanishing shear and twist scalars.

These are all principle null geodesic congruences in the sense that their contracting or expanding wavefronts are geometric spheres belonging to the system [itex]\tau = \tau_0,\; r=r_0[/itex]. Furthermore, we see that our radial coordinate r has a very important physical interpretation which shows that these congruences behave locally just like the familiar null geodesic congruences in Minkowski vacuum in which spherical wavefronts contract (expand) from some point in spherically symmetric fashion.

Studying these null geodesic congruences suggests adopting new coordinates in which the world sheets of the expanding or contracting wavefronts are "straightened". This leads to the outgoing and ingoing Eddington charts respectively (see Post #8). These are very useful for several purposes, but they cover the same domains as the outgoing and ingoing Painleve charts, so don't advance us in finding a conformally compactified chart.

But recall that the Schwarzschild chart on the exterior region is time symmetric. Following what I said in Post #2 about the general trick, we should first transform this to a double null version (which covers the same domain), and then compactify. It turns out that we can do this in such a way that we eliminate the coordinate singularity at [itex]r=2m[/itex]. The result is the double null version of the Penrose chart
[tex]
\begin{array}{rcl}
ds^2 & = & - \frac{64 m^2 \, (1-2m/r)}{\sin(2p) \, \sin(2q)} \; dp \, dq + r^2 \, d\Omega^2 \\
r & = & 4m \; \left( 1+ W\left( \frac{\tan(p) \, \tan(q)}{2m} \right) \right), \\
&& -\pi/2 < p,q < \pi/2, \; \tan(p) \, \tan(q) > -2m/e
\end{array}
[/tex]
where W is (a real valued branch of) the Lambert W function, which is defined as the inverse function of [itex]z \rightarrow z \, \exp(z)[/itex]. Here, [itex]\partial_p[/itex] is future pointing null, while [itex]\partial_q[/itex] is past pointing null. See the figures below, where in the right exterior region p points up and right while q points down and right.

You might think that the coefficient of [itex]dp \, dq[/itex] vanishes at r=2m, but plugging in the given expression for r (as a function of our null coordinates p,q) and taking the limit [itex]q \rightarrow 0^+[/itex] shows that it does not!

(Pedantic note: for the double null Penrose chart in the form I just gave, the past curvature singularity actually bows up slightly while the future curvature singularity bows down slightly. It is conventional to sketch the Penrose diagrams with straight segments instead of slightly bowed curves.)

In this Penrose chart the ingoing Lemaitre frame (defined on the right exterior and future interior regions) becomes
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & \frac{1}{8m} \; \left( \frac{\sin(2p)}{1+\sqrt{2m/r}} \; \partial_p
- \frac{\sin(2q)}{1-\sqrt{2m/r}} \; \partial_q \right) \\
\vec{e}_2 & = & \frac{1}{8m} \; \left( \frac{\sin(2p)}{1+\sqrt{2m/r}} \; \partial_p
+ \frac{\sin(2q)}{1-\sqrt{2m/r}} \; \partial_q \right) \\
\vec{e}_3 & = & \frac{1}{r} \;\partial_\theta \\
\vec{e}_4 & = & \frac{1}{r \; \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
Again, at first glance it appears this becomes singular at r=2m, but plugging in the expression for r and taking the limit [itex]q \rightarrow 0^+[/itex] shows that the frame is perfectly well behaved at the horizon. Indeed, on [itex]q=0, \; 0 < p < \pi/2[/itex] the frame becomes
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & \frac{\sin(2p)}{16m} \; \partial_p - \cot(p) \; \partial_q \right) \\
\vec{e}_2 & = & \frac{\sin(2p)}{16m} \; \partial_p + \cot(p) \; \partial_q \right) \\
\vec{e}_3 & = & \frac{1}{2m} \;\partial_\theta \\
\vec{e}_4 & = & \frac{1}{2m \; \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]

For completeness, the static frame (defined on the right exterior region) is
[tex]
\begin{array}{rcl}
\vec{h}_1 & = & \sqrt{1-2m/r} \; \partial_t
= \frac{1}{8m \, \sqrt{1-2m/r}} \; \left( \sin(2p) \; \partial_p - \sin(2q) \; \partial_q \right) \\
\vec{h}_2 & = & \frac{1}{\sqrt{1-2m/r}} \; \partial_r
= \frac{1}{8m \, \sqrt{1-2m/r}} \; \left( \sin(2p) \; \partial_p + \sin(2q) \; \partial_q \right) \\
\vec{h}_3 & = & \frac{1}{r} \;\partial_\theta \\
\vec{h}_4 & = & \frac{1}{r \; \sin(\theta)} \; \partial_\phi
\end{array}
[/tex]
This frame really does blow up at r=2m!

Now transforming the null coordinates to new timelike and spacelike coordinates T,R gives the conformally compactified chart for the Schwazschild vacuum given in most textbooks. I usually just use the double null form, however.

See the figure below for a sketch of the contours of r plotted in the Penrose diagram, and notice that these contours are also the flow lines of the Killing flow [itex]\partial_\tau[/itex] (if we supress the angular coordinates).

In the next figure, I have sketched "constant time" hyperslices in the future interior and right exterior Schwarzschild charts. The exterior slice is of course one sheet of the Flamm paraboloid, and the "opposing" principle null geodesic congruences have spherical wavefronts which expand/contract just as in ordinary spacetime. The interior slice has the "hypercylindrical" geometry of [itex]\mathbb{R} \times S^2[/itex], with the spherical factor shrinking as proper time increases, and the "opposing" principle null geodesic congruences are both contracting, with spherical wavefronts traveling in opposite directions along the "cylinder". (Compare the figures in Post #8.) If you find it hard to knit together these very different pictures at r=2m, that is my point--- its a bad idea to try to avoid using the Penrose diagram when you are trying to understand the global causal structure!

Finally, I have sketched the world line of a typical infalling Lemaitre observer and shaded the region covered by the ingoing Painleve chart, the ingoing Eddington chart, and various other ingoing charts.

Figures: left to right:

• contours of the radial coordinate r (left) and Killing flow for [itex]\partial_t[/itex] (right); this Killing flow corresponds to time translation in the exterior regions but to a spatial translation (along a hypercylinder) in the interior regions,
• comparing principle null geodesic congruences in right exterior and future interior regions; for each region, I have sketched the appearance of the "opposing" wavefronts in a "constant time" spatial hyperslice in the interior/exterior Schwarzschild charts,
• region covered by infalling Painleve chart (or ingoing Eddington chart) and world line of a typical Lemaitre observer.

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. III. Schwarzschild vacuum (cont'd)

(cont'd)

As a futher invitation to SA/Ms to see how neatly the Penrose diagram visually summarizes the relationship between various useful coordinate charts defined on different regions, study the first figure below. Notice that the locus q=0 is the diagonal line running from lower left to upper right, i.e. a sequence of spheres all having the same surface area [itex]16 \pi \, m^2[/itex], but the region r=2m in the static chart corresponds to a single such sphere, which is why these charts depict the world lines of infalling particles as "bending upwards and becoming asymptotic to r=2m". In fact, these world lines cross the locus q=0 at some p > 0.

Next, compare the second figure with the discussion of the principle null geodesic congruences in the ingoing Lemaitre chart in Post #7. This brings out the way that as we cross the event horizon (from right exterior to future interior), the expanding congruence is exchanged for another contracting congruence. In the exterior regions (as in Minkowski vacuum) we have one expanding and one contracting principle null geodesic congruence (whose wavefronts are expanding/contracting spheres). But in the future interior region both are contracting, and in the past interior, both are expanding. This phenomenon, in which the sign of the optical expansion scalar flips, shows that in the Schwarzschild vacuum, the event horizon is also an apparent horizon. In models in which a static nonspinning black hole is formed by the gravitational collapse of dust or "null dust" (massless radiation), the apparent horizon will usually be a distinct locus from the event horizon, except in regions where the hole is locally isometric to the Schwarzschild vacuum.

Recalling that in our Penrose diagrams, line segments with slope +/-1 correspond to null geodesics in one of the principle null geodesic congruences, you can see how to draw arbitrarily many spatial hyperslices. As an exercise, recalling that each point in the Penrose diagram corresponds to a round sphere of some surface area, and that all these spheres are nested in spherically symmetric fashion, see if you can sketch axially symmetric embeddings (with one spatial dimension suppressed) of some such hyperslices.

Figures: left to right:

• Regions of the maximal analytic extension covered by various charts:
  • top left: ingoing charts (with the world lines of some ingoing Lemaitre observers):
    • ingoing Eddington
      [tex]
      ds^2 = -(1-2m/r) \, du^2 + 2 \, du \, dr + r^2 \, d\Omega^2
      [/tex]
    • ingoing Painleve
      [tex]
      ds^2 = -(1-2m/r) \, d\tau^2 + 2 \, \sqrt{2m/r} \, d\tau \, dr + dr^2 + r^2 \, d\Omega^2
      [/tex]
    • ingoing Lemaitre
      [tex]
      ds^2 = -d\tau^2 + (4m/3)^{2/3} \, (\rho-\tau)^{2/3} + (9m/3)^{2/3} (\rho-\tau)^{4/3} d\Omega^2
      [/tex]
  • top center: right exterior (with the world lines of some static observers)
    • Schwarzschild exterior
      [tex]
      ds^2 = -(1-2m/r) \, dt^2 + \frac{dr^2}{1-2m/r} + r^2 \, d\Omega^2
      [/tex]
    • spatially isotropic
      [tex]
      ds^2 = - \, \left( \frac{1-\frac{m}{2 \, \bar{r}}}{1+\frac{m}{2 \,\bar{r}}} \right)^2 \, dt^2
      + \left( 1+\frac{m}{2 \, \bar{r}} \right)^4 \; \left( d\bar{r}^2 + \bar{r}^2 \, d\Omega^2 \right)
      [/tex]
    • exterior Costa
      [tex]
      ds^2 = - \, \frac{\tanh(\zeta/2)^2}{2m} \, dt^2 + \frac{\cosh(\zeta/2)^4}{2m} \; \left( d\zeta^2 + d\Omega^2 \right)
      [/tex]
      (notice that [itex]d\sigma^2 = d\zeta^2 + d\Omega^2[/itex] is the line element of the Riemannian hypercylinder [itex]\mathbb{R} \times S^2[/itex]),
    • Weyl canonical (rational prolate spherical version)
      [tex]
      ds^2 = -\frac{x-1}{x+1} \, dt^2 + \frac{x+1}{x-1} \; \left( dx^2 + (x^2-1)
      \; \left( \frac{dy^2}{1-y^2} + (1-y^2) \, d\phi^2 \right) \right)
      [/tex]
  • top right: outgoing charts (with the world lines of some outgoing Lemaitre observers)
    • outgoing Eddington
      [tex]
      ds^2 = -(1-2m/r) \, dv^2 - 2 \, dv \, dr + r^2 \, d\Omega^2
      [/tex]
    • outgoing Painleve
      [tex]
      ds^2 = -(1-2m/r) \, d\tilde{\tau}^2 - 2 \, \sqrt{2m/r} \, d\tilde{\tau} \, dr + dr^2 + r^2 \, d\Omega^2
      [/tex]
    • outgoing Lemaitre
      [tex]
      ds^2 = -d\tilde{\tau}^2 + (4m/3)^{2/3} \, (\rho+\tilde{\tau})^{2/3}
      + (9m/3)^{2/3} (\rho+\tilde{\tau})^{4/3} d\Omega^2
      [/tex]
  • bottom center: future interior region (with the world lines of some Frolov observers)
    • Schwarzschild future interior
      [tex]
      ds^2 = - \, \frac{d\bar{t}^2}{2m/\bar{t}-1} + (2m/\bar{t}-1) \, dz^2 + \bar{t}^2 \, d\Omega^2
      [/tex]
      (awkwardly enough, the range [itex]0 < \bar{t} < 2m[/itex] reverses the direction of increasing proper time of Frolov observers)
    • interior Costa
      [tex]
      ds^2 = \frac{\cos(\psi/2)^4}{2m} \; \left( -d\psi^2 + d\Omega^2 \right) + \frac{\tan(\psi/2)^2}{2m} \, dz^2
      [/tex]
      (notice that [itex]d\sigma^2 = -d\psi^2 + d\Omega^2[/itex] is the line element of a Lorentzian hypercylinder).
• Apparent horizons separate expanding and contracting principle null geodesic congruences; the figure shows some world sheets of expanding or contracting spherical wavefronts together with the sign of the optical expansion scalar (positive for expanding wavefronts; negative for contracting wavefronts).

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. IV. Some Gravitational Collapse Models

General relativity is a more accurate and hence more realistic theory of gravitation than Newtonian gravitation. (In particular, gtr demands that "field updating information" propagate at the speed of light, thus meeting an objection raised by Newton himself to the implausible notion of "action at a distance".) It follows that some idealizations which are useful and work well in Newtonian gravitation either won't exist at all in gtr, or will have unexpected properties due to the fact that we are posulating at overidealization in gtr (but not in Newtonian gravitation).

Thus, we should not be particularly disturbed that the Schwarzschild vacuum, which we uncovered by searching for a spherically symmetric vacuum solution (with, tacitly, an asymptotically flat exterior sheet, so that we are trying to find a model of an "isolated spherically symmetric massive object"), turns out to have a rather unphysical global structure. As everyone here probably knows, realistic applications of (portions of) the Schwarzschild vacuum in gtr arise principally in two ways:

• the class of static spherically symmetric perfect fluid solutions is known in closed form (sort of), and any ball of fluid can be matched across its zero pressure surface to a portion of the Schwarzschild vacuum (covering the exterior sheet with a ball removed; this ball must of course have [itex]r=r_0[/itex] with[itex]r_0 > 2m[/itex], in fact by Buchdahl's theorem a bit bigger than this bound suggests),
• models of the formation of a static nonspinning black hole by the gravitational collapse of dust balls, shells of null dust, massless scalar field, or more elaborate scenarios.

The first of these gives models of isolated static objects which never form a black hole; the second class is the one we are interested in here.

The simplest realistic (more or less) model of the formation of a black hole by gravitational collapse is the Oppenheimer-Snyder model, in which a ball of FRW dust (a region cut out of the FRW dust with E^3 hyperslices) collapses "from a state of rest with infinite surface area", where we match across the collapsing spherical surface to a region of the Schwarzschild vacuum. See figure below, where the dust filled region is shaded. Note the formation of a strong spacelike curvature singularity (top left). We can also see how an apparent horizon forms and meets the event horizon at the surface. I have shown a sphere of outgoing EM radiation which is initially expanding from the center of the dust ball (dotted world sheet in the diagram), and which meets the apparent horizon inside the event horizon. The wavefronts belonging to the principle outgoing null geodesic congruence actually start contracting (negative optical expansion scalar) after they meet the apparent horizon. But signals from r=0 at any time before this dust particle meets the final curvature singularity do expand at least initially, so the apparent horizon must bend down and over as shown. This behavior of typical of apparent horizons.

Note well: unlike the event horizon, which is defined by a global condition (not verifiable by any local measurement), apparent horizons are defined by a local property (a principle null geodesic congruence exists and its optical expansion scalar changes sign).

In the figure, the dashed curve suggests the radial motion of an observer who remains outside the surface of the dust ball and avoids falling into the newly formed hole, either because he is firing his rocket engine radially inwards or because he has nonzero angular momentum wrt the hole (in which case there is some angular motion which is not shown in the two-dimensional Penrose diagram).

An even simpler collapse model is obtained by starting with the ingoing Eddington chart
[tex]
ds^2 = -(1-2m/r) \, du^2 + 2 \, du \, dr + r^2 \, d\Omega^2
[/tex]
and letting m be a monotonically increasing function of u. This gives an exact null dust solution, in which nonzero components of the Einstein tensor occur only at events where dm/du > 0. They arise from the mass-energy and momentum of massless radiation, which we can usually interpret as incoherent EM radiation. (Pedantic note: we cannot make the Vaidya null dust into an exact Einstein-Maxwell solution with a null EM field, but that isn't really a problem, it just means that the radiation is massless but doesn't form a coherent EM wave). Then we can start with a Minkowski region (m=0) and at a certain u start smoothly increasing m, and we can also assume m remains constant after some later u. This gives a model in which a thick spherical shell of massless radiation is contracting (at the speed of light, at the level of tangent spaces) around a Minkowski bubble, and surrounded by a Schwarzschild region (with mass parameter corresponding to the final value of m). See the figure below.

In the figure, the dashed curve labeled L (for "lucky") denotes the world line of an observer who initially believes he is living in Minkowski vacuum. Boooriiing! Fortunately, along comes a little entertainment, a collapsing spherical shell of massless radiation which focuses on the locus r=0. As the shell passes, our observer measures tidal forces and after a while finds he is outside a newly formed black hole. But now consider the dashed curve labeled U (for "unlucky"), which denotes the world line of an observer who happens to be a bit closer to r=0. He too initially believes he is living in Minkowski vacuum, and r=0 is not even a distinguished place yet. Bye and bye along comes the collapsing spherical shell. After a short time our observer finds he is outside a massive object and falling inwards (decreasing r), and to his horror, he finds he is unable to escape. Shortly later, his world line approaches the strong spacelike curvature singularity in his immediate future and he meets his gruesome demise.

In the figure, the dotted curve denotes the world sheet of a wavefront belonging to the outgoing principle null geodesic congruence. Where this meets the apparent horizon (bold curve), the optical expansion scalar changes sign from positive to negative, so after that, the wavefront is actually collapsing, even though at the level of tangent spaces it is "outgoing at the speed of light". This is the characteristic property of a spacetime region containing trapped surfaces.

Of course, observation and experience suggests that it is not easy to arrange for a shell of intense massless radiation to form and collapse in a perfectly spherical manner, so this thought experiment cannot be understood as a prediction that it is possible to make a black hole in this manner! Rather, this little thought experiment (from the monograph of Frolov and Novikov) is intended to illustrate the "teleological" nature of the event horizon; it depends on the entire future history of the spacetime. In our example, neither L or U could have had any clue that a spherical shell of massless radiation is approaching their location, for it is collapsing at the speed of light.

It will be good practice to sketch some contour lines for r in the last two Penrose diagrams. Note that due to the proximity of the final singularity (r=0) and Scri^+ near the point i^+, all the contour lines must meet i^+! Similarly for i^-,

The third figure shows that Vaidya collapse models have another surprise in store: if the massless radiation accumulates slowly enough, we obtain a model with a more complicated global structure, including a null singularity. This kind of model includes a Cauchy horizon; inside this locus, roughly speaking, gtr acknowledges that given reasonable initial data (think "Cauchy problem") it cannot yield a unique solution. This is a genuine and serious flaw in what is otherwise an amazingly marvelous relativisitic field theory! But we can at least say that this uncertainty about what will happen next is confined inside the Cauchy horizon.

Figures: left to right:

• the Oppenheimer-Snyder collapsing dust ball
• a simple Vaidya model (collapsing shell of null dust)
• various types of Vaidya collapse models

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. IV. Some Grav Collapse Models (cont'd)

(cont'd)

For additional practice in "reading" Penrose diagrams, I offer some more Penrose diagrams.

The first shows another simple collapse model obtained by matching a portion of the FRW dust with S^3 hyperslices to a portion of the Schwarzschild vacuum; this model features a dust ball which expands from an initial curvature singularity through its "white hole horizon", reaches a maximal size, then falls back through its "black hole horizon" and forms a final curvature singularity.

Like the models shown in the previous three figures, the Penrose diagram of this model includes a point labeled i^0, which means it has an asymptotically flat exterior sheet. (The maximal analytical extension of the Schwarzschild vacuum has two exterior sheets, so it has two different points labeled i^0.)

The next Penrose diagram depicts a model which lacks an asymptotically flat exterior sheet, specifically a recent "two-center" model of Ellis et al., which is formulated on de Sitter background. It features two OS-like dust balls which collapse and form two black holes, and it includes cosmological horizons as well as event horizons.

The third figure depicts the Penrose diagram for a Maeda wormhole model constructed by matching a portion of the Roberts minimally coupled massless scalar field solution to portions of two different Minkowski vacuums (!). The two dashed curves indicate the world lines of two observers, each beginning his existence in one of the two Minkowski regions. The right observer initially believes he is living in Minkowski vacuum, but after a time he encounters a spherically collapsing region filled with a massless scalar field. After some time he can for the first time receive signals from the left observer, and some considerable time after that he has a rendevous with the left observer, who tells a very different story: he too initially believed he was living in Minkowski vacuum, but after a certain time he encountered a spherically expanding region filled with massless scalar field, with spherical shells expanding from a certain point, and he could immediately receive signals from the right observer.

One interesting feature of this model is that the sphere where the two Minkowski regions appear to "meet' is actually a curvature singularity, but everywhere else the curvature is finite!

I should stress again that none of these models (not even the OS dust, not really) is intended as a serious model of a realistic gravitational collapse scenario. Rather, they are thought experiments which suggest various possibilities we need to consider when we study gravitational collapse.

Figure: left to right:

• an expanding and recollapsing dust ball
• a lambdadust ([itex]\Lambda > 0[/itex]) model with two collapsing dust balls
• a Maeda wormhole (collapsing shells of massless scalar field)

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. V. Some Stnry Axisym Exms

Spacetimes which are stationary and closedly related to the Schwarzschild vacuum are commonly encountered in PF posts. In this post I will display the Penrose-Carter diagrams of six examples of such spacetimes, which you can practice "reading". If you get stuck or are curious about one of the models sketched here, see Griffiths and Podolsky, Exact Space-Times in Einstein's General Relativity, Cambridge University Press, 2009.

First, two useful reminders about phenomena not directly concerned with conformal structure:

Recall that if a spacetime (M,g) possesses a Killing vector field [itex]\xi[/itex], the integral curves are each either timelike, null, or spacelike. If on some open neighborhood U in M, all the integral curves are timelike, then our Killing vector field expresses time translation symmetry and we say that U is a stationary region. If in addition, [itex]\xi[/itex] is an irrotational (vorticity-free) vector field, we say that U is a static region (because in this case U can be foliated with spatial hyperslices everywhere orthogonal to the integral curves of our Killing vector field).

Recall too that solutions are usually found first as local solutions defined on some U, and are then analytically extended to some larger spacetime. Maximal analytic extensions are usually not unique; this happens to be true for the Schwarzschild vacuum but is not for the Schwarzschild-de Sitter lambdavacuum, for example. (Below I sketch the conformal structure of a minimal maximal analytic extension of the Schwarzschild de Sitter lambdavacuum, i.e. the simplest possibility drawn from an infinite family of possible maximal extensions.)

In each figure below,

• each spacetime depicted contains various regions, some static, some not; some but not all of the static regions are asymptotically flat sheets "exterior" to an event horizon,
• the "perimeter" of each diagram may feature (in case of an asymptotically flat sheet) "null surfaces at conformal infinity" and a "sphere at spatial infinity", and also may feature past/future curvature singularities,
• some of these models feature strong spacelike curvature singularities, and some feature strong timelike singularities; roughly speaking, only the former are thought to resemble what you might actually encounter inside a black hole in Nature,
• inside each diagram, various regions are separated by horizons of various kinds, including event horizons, Cauchy horizons, and cosmological horizons; there are also apparent horizons in the black hole regions, but in these overidealized examples, the apparent horizons mostly coincide with event horizons so they are not shown,
• the angular coordinates are supressed, so "points" in these diagrams represent Riemannian two spheres,
• lines with slope +/-1 represent (supressing angular variables) radial null geodesics; more properly, each such line represents a world sheet modeling the history of a Riemannian two-sphere which expands or contracts "at the speed of light",
• dashed lines represent surfaces of constant Schwarzschild radial coordinate, and should suggest the integral curves of a certain Killing vector field (timelike on the stationary regions in each spacetime); these integral curves foliate the surfaces of constant r coordinate,
• all of these spacetime models are overidealized in various ways, and the conformal structure of our universe--- which is full of black holes--- is not thought to resemble these models very closely inside each black hole; in particular: while the "no hair theorems" state that the exterior of a black hole must closely resemble the Kerr vacuum there, the interior need not.

Figures (left to right): Penrose-Carter diagram for

• Schwarzschild vacuum (models nonrotating black hole immersed in Minkowski background; has two asymptotically flat exterior sheets) and Schwarzschild-de Sitter lambdavacuum (models nonrotating black hole immersed in de Sitter background; has two asympotically de Sitter exterior sheets).
• Reissner-Nordstrom electrovacuum (models nonrotating charged black hole immersed in Minkowski background; has infinitely many asymptotically flat exterior sheets) and Reissner-Nordstrom de Sitter lambda-electrovacuum (models nonrotating charged black hole in de Sitter background; has infinitely many asymptotically de Sitter exterior sheets); both diagrams extend infinitely upwards and downwards; the left figure includes the world line of an observer who passes from one exterior sheet into another.
• Kerr vacuum (models rotating black hole immersed in Minkowski background; has infinitely many asymptotically flat positive Komar mass exterior sheets and also infinitely many asymptotically flat negative Komar mass interior sheets) and Taub-NUT vacuum (models a nonrotating black hole which has no curvature singularities, but whose exterior sheets are not asympotically flat); in the figures, some exterior sheets are labeled; both diagrams extend infinitely upwards and downwards; the left figure includes the world line of an observer who passes from one exterior sheet into another. (In the lefthand figure, contrary to what the figure seems to suggest, the timelike singularity is the world sheet of a ringlike curve, and particles can easily pass through this locus to access the rest of the interior sheet.)

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VI. Evaporating Black Holes

As I write, it must be the weekend when returning students arrive in dorm rooms in the English speaking schoolworld, because suddenly many posts from curious newbies have appeared in the relativity subforum. Among the most common newbie quesions--- they almost always appear at this time of year--- concern evaporating black holes. These questions are often inspired by (badly written and misleading) press releases from university PR hacks touting some (typically mundane) paper by one of their faculty as an alleged "revolutionary advance" which "helps resolve old mysteries concerning evaporating black holes", or some claim like that.

Clearly in this post I cannot hope to even pretend to adequately address the genuine mysteries currently associated with the notion of evaporating black holes, but I should at least remind readers that the notions of Hawking radiation and evaporating black holes are grounded in the so-called semiclassical approximation, a formalism for doing quantum field theory computations on a curved spacetime. Unfortunately this formalism is not entirely well grounded, and it is quite tricky, although the oldest and best known results (due to Hawking in the late 1970s) do seem to have held up well.

For the purposes of understanding very roughly how quantum effects might dramatically alter our understanding of "the big picture", if and when haplass humans ever succeed in not only creating a viable quantum theory of gravitation, but in learning how to compute with it sufficiently well to make unambiguous predictions, it is useful to know that sometimes quantum considerations give rise to an "effective field theory" approximation in classical physics, and sometimes suggest Carter-Penrose diagrams sketching possible conformal structure which might be associated with a model formulated using some effective field theory.

I think it is fair to say that currently, few gravitation physicists doubt that black holes should in principle evaporate by some mechanism which reduces in an appropriate limit to that suggested by Hawking. As everyone knows, I guess, if this is true it raises many new questions, which are currently wide open. One of these open questions is whether anything is left behind when a black hole evaporates: a timelike curvature singularity? Some other kind of geometrically meaningful singularity? Something even stranger, perhaps?

A short book with a very long title which advocates a particular point of view (neccessarily controversial at present, since no-one really knows what they are talking about yet!), but which also offers some good introductory chapters, is Susskind, An Introduction to Black Holes, Information and the String Theory Revolution: the Holographic Universe, World Scientific, 2005. This might be a good place to start reading if anyone is curious to learn more.

At this point, I'll simply drop two slightly different Carter-Penrose diagrams which have been suggested as possible approximation representations of what "the big picture" for an evaporating black hole might look like. Neither figure attempts to answer the question about black hole remnants!

Compare the apparent horizon depicted in the two suggestions. Why is the older suggestion at left far less radical than the newer suggestion at right?

Figure:

• two Carter-Penrose diagrams representing suggested conformal structures for an isolated evaporating black hole in Minkowski background; in both figures, an apparent horizon is shown as a short bold curve inside the black hole interior region; the left figure also includes the "ordinary stellar matter" which originally formed the black hole.

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VII. Cosmological Models

Switching gears, let me turn aside from the mysteries of black holes and briefly sketch the conformal structure of the most commonly encountered cosmological models.

In this post, I'll just drop sketches of the conformal structure of some FRW dust models; see Griffiths and Podolsky for details and for similar diagrams for the FRW radiation fluid models.

Figures (left to right):

• Some FRW dusts with [itex]\Lambda = 0[/itex]
• Some FRW dusts with [itex]\Lambda > 0[/itex]; in the left hand figure, notice that there is no singularity at top!
• An FRW dust with [itex]\Lambda < 0[/itex]; notice the singularity at top!

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VII. Cosmological Models (cont'd)

(continued)

One of the benefits of getting in the habit of sketching conformal structures is that this can clarify important problems.

One simple example in the context of cosmology is the "horizon problem". Prior to a certain epoch, the universe was so hot and dense that photons could not fly freely; the CMB is the modern artifact of "the moment" when photons could first propagate freely. And the CMB is observed to be impressivly homogeneous. The problem arises when you consider the absolute future of events E, E' before "the moment" when photons could first fly free (see figure below). Even ignoring that fact that photons could not move freely below "the" hyperslice in question (dashed line), the absolute future of E, E' do not intersect until a much later epoch, so we should apparently expect the CMB associated with different regions of the night sky (mentally rotate the figure, and then mentally replace the circle where the absolute past of "Here and Now" intersects "photons fly free" with a Riemannian two-sphere) to be quite different, in striking contrast to observation.

The McVittie static spherically symmetric perfect fluid is an interesting exact solution which models a (nonrotating, uncharged) black hole immersed in a static spherically symmetric perfect fluid whose metric tensor at large distances from the hole approaches the metric of an FRW dust with E^3 hyperslices. While this solution is not realistic, it is pedagogically useful. Below I sketch the conformal structure together with an apparent horizon which mediates between the black hole dominated region (at left) and the FRW dominated region (at right); that is, this apparent horizon is the locus where a principle null geodesic congruence (spherically symmetrically expanding/collapsing wavefronts) changes from expanding (FRW behavior) to contracting ("radially contracting" congruence in black hole exterior). See the figure below, and find the future interior black hole region, the exterior but black hole dominated region (outside the event horizon and inside the apparent horizon), and the exterior FRW dominated region (outside the apparent horizon but inside the cosmological horizon), and make sure you understand the signs of the optical expansion scalars of the principle geodesic null congruences indicated in the figure!

(I wanted to give a citation here but seem to have lost it! I'll try to find it and add it later.)

Figures (left to right):

• Sketch illustrating the horizon problem in cosmological problems featuring a Big Bang (an initial curvature singularity).
• Conformal structure of the McVittie static spherically symmetric perfect fluid, which "interpolates" between the Schwarzschild vacuum and FRW dust with E^3 hyperslices.

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VIII. Plane-Symmetric Spacetimes

So far most of the spacetime models I have discussed have been featured a family of nested two-spheres expressing spherical symmetry, or at least axisymmetry. They have been models of things like isolated black holes, or homogeneous cosmological models in which it is often possible and convenient to introduce an arbitrarily chosen "center of spherical symmetry". In such cases, one is always on the lookout for possible asympotically flat sheets (for places where the spacetime geometry approaches the geometry of Minkowski vacuum).

But of course other types of symmetry occur and are sometimes important in general relativity. Indeed, some of the most interesting and informative conformal diagrams concern not spherically symmetric spacetimes, but

• colliding plane wave spacetimes (planar symmetry)
• models featuring a pair of accelerating massive objects (boost-rotation symmetry)

In this post I want to discuss the former possibility. In this case, points in two-dimensional Carter-Penrose diagrams (with the "inessential" planar coordinates suppressed) will represent euclidean two-planes, not round Riemannian two-spheres.

(Since the euclidean plane is not compact, strictly speaking I am now talking about "partial compactifications", but since we will be mostly ignoring the planar variables, this makes little difference in studying the conformal structure.)

First, as a warmup: two of the simplest exact vacuum solutions are

• the Kasner vacuum with planar symmetry (a special case of the more general Kasner vacuums, which is turn a special case of the Kasner dusts),
  [tex]
  \begin{array}{rcl}
  ds^2 & = & -dt^2 + t^{4/3} \; \left( dx^2 + dy^2 \right)
  + t^{-2/3} \; dz^2 \\
  && 0 < t < \infty, \; -\infty < x, \, y, \, z < \infty
  \end{array}
  [/tex]
• the Taub static plane symmetric static vacuum, also known as the Levi-Civita type AIII static vacuum
  [tex]
  \begin{array}{rcl}
  ds^2 & = & -z^{-2/3} \; dt^2 + z^{4/3} \; \left( dx^2 + dy^2 \right)
  + dz^2 \\
  && 0 < z < \infty, \; -\infty < t, \, x, \, y, < \infty
  \end{array}
  [/tex]
  (discovered by Levi-Civita c. 1919, rediscovered by Kasner in 1921, then rediscovered again by Taub in 1951, but best known under the name of Taub).

both of which are Petrov type D vacuum solutions. There are literally dozens of charts for each of these which have been employed by various authors in the literature, from which I have chosen two of the simplest, which manifestly display the very close relation between these solutions.

The Kasner type D vacuum is dynamical; it features a Big Bang type initial curvature singularity at t=0, followed by homogeneous but anisotropic expansion. (As already mentioned, the Kasner vacuums are a special case of the Kasner dusts, which are simple cosmological models which are homogeneous but anisotropic; the vacuum case arises as the zero dust density limit of the dust solutions.) The Taub type D vacuum is static and both inhomogeneous and anisotropic; it features a timelike strong curvature singularity at z=0. See the figures below.

For those of you who use Ctensor under Maxima, here are two Ctensor files you can run in batch mode under wxmaxima. These files instruct Maxima to compute the frame field components of the Riemann tensor, and also the Weyl spinors using NP formalism and the Petrov type of the Weyl tensor (agrees with Riemann tensor, since these are vacuum solutions).

Here is the Kasner plane symmetric vacuum:

/* 
Kasner vacuum with E^2 symmetry; comoving Cartesian chart; nsi coframe 

*/
load(ctensor);
cframe_flag: true;
ratchristof: true;
ctrgsimp: true;
/* define the dimension */
dim: 4;
/* list the coordinates */
ct_coords: [t,x,y,z];
/* define background metric */
lfg: ident(4);
lfg[1,1]: -1;
/* define the coframe */
fri: zeromatrix(4,4);
fri[1,1]: -1;
fri[2,2]:  t^(2/3);
fri[3,3]:  t^(2/3);
fri[4,4]:  t^(-1/3);
/* declare K to be constant */
declare(K, constant);
/* setup the spacetime definition */
cmetric();
/* display matrix whose rows give coframe covectors */
fri;
/* compute a matrix whose rows give frame vectors */
fr;
/* metric tensor g_(ab) */
lg;
/* compute g^(ab) */
ug: invert(lg);
christof(false);
/* Compute fully covariant Riemann components R_(mijk) = riem[i,k,j,m] */
lriemann(true);
/* Compute R^(mijk) */
uriemann(false);
/* Compute Ricci componets R_(jk) */
ricci(true);
/* Compute trace of Ricci tensor */
tracer;
/* Compute R^(jk) */
uricci(false);
/* Compute and display MIXED Einstein tensor G^a_b */
/* For (-1,1,1,1) sig Flip sign of top row to get G^(ab) */
einstein(false);
cdisplay(ein);
/* WARNING! leinstein(false) only works for metric basis! */
/* Compute Kretschmann scalar */
factor(radcan(rinvariant()));
print("Above: Kretschmann scalar");
/* Einstein tensor as matrix */
matrix([ein[1,1],ein[1,2],ein[1,3],ein[1,4]],
[ein[2,1],ein[2,2],ein[2,3],ein[2,4]],
[ein[3,1],ein[3,2],ein[3,3],ein[3,4]],
[ein[4,1],ein[4,2],ein[4,3],ein[4,4]]);
print("Above: Einstein tensor; flip sign of top row!");
/* electroriemann tensor */
factor(matrix([lriem[2,2,1,1], lriem[2,3,1,1],lriem[2,4,1,1]],
[lriem[3,2,1,1],lriem[3,3,1,1],lriem[3,4,1,1]],
[lriem[4,2,1,1],lriem[4,3,1,1],lriem[4,4,1,1]]));
print("Above: electroriemann tensor or tidal tensor");
/* magnetoriemann tensor */
factor(matrix([lriem[2,4,3,1],lriem[2,2,4,1],lriem[2,3,2,1]],
[lriem[3,4,3,1],lriem[3,2,4,1],lriem[3,3,2,1]],
[lriem[4,4,3,1],lriem[4,2,4,1],lriem[4,3,2,1]]));
print("Above: magnetoriemann tensor");
/* Construct NP tetrad for our frame, compute Weyl spinors and Petrov type */
nptetrad(true);
weyl(false);
psi(true);
factor(psi[0]);
factor(psi[1]);
factor(psi[2]);
factor(psi[3]);
factor(psi[4]);
petrov();

Here is the Taub plane symmetric static vacuum:

/* 
Taub plane symmetric vacuum; 
aka Levi-Civita type A3 static vacuum (Petrov type D); 
aka Weyl vacuum from "Taub ray" potl; 
aka Weyl vacuum from "Taub rod" potl

Compare the Kasner plane symmetric vacuum, which is also Petrov type D,
but dynamical.

*/
load(ctensor);
cframe_flag: true;
ctrgsimp: true;
/* define the dimension */
dim: 4;
/* list the coordinates */
ct_coords: [t,x,y,z];
/* define background metric */
lfg: ident(4);
lfg[1,1]: -1;
/* define the coframe */
fri: zeromatrix(4,4);
fri[1,1]: -z^(-1/3);
fri[2,2]:  z^(2/3);
fri[3,3]:  z^(2/3);
fri[4,4]:  1;
/* setup the spacetime definition */
cmetric();
/* display matrix whose rows give coframe covectors */
fri;
/* compute a matrix whose rows give frame vectors */
fr;
/* metric tensor g_(ab) */
lg;
/* compute g^(ab) */
ug: invert(lg);
christof(false);
/* Compute fully covariant Riemann components R_(mijk) = riem[i,k,j,m] */
lriemann(true);
/* Compute R^(mijk) */
uriemann(false);
/* Compute Ricci componets R_(jk) */
ricci(true);
/* Compute trace of Ricci tensor */
tracer;
/* Compute R^(jk) */
uricci(false);
/* Compute and display MIXED Einstein tensor G^a_b */
/* For (-1,1,1,1) sig Flip sign of top row to get G^(ab) */
einstein(false);
/* WARNING! leinstein(false) only works for metric basis! */
/* Einstein tensor as matrix */
factor(matrix([ein[1,1],ein[1,2],ein[1,3],ein[1,4]],
[ein[2,1],ein[2,2],ein[2,3],ein[2,4]],
[ein[3,1],ein[3,2],ein[3,3],ein[3,4]],
[ein[4,1],ein[4,2],ein[4,3],ein[4,4]]));
/* Kretschmann scalar */
factor(radcan(rinvariant()));
/* electroriemann tensor */
matrix([lriem[2,2,1,1], lriem[2,3,1,1],lriem[2,4,1,1]],
[lriem[3,2,1,1],lriem[3,3,1,1],lriem[3,4,1,1]],
[lriem[4,2,1,1],lriem[4,3,1,1],lriem[4,4,1,1]]);
/* magnetoriemann tensor */
matrix([lriem[2,4,3,1],lriem[2,2,4,1],lriem[2,3,2,1]],
[lriem[3,4,3,1],lriem[3,2,4,1],lriem[3,3,2,1]],
[lriem[4,4,3,1],lriem[4,2,4,1],lriem[4,3,2,1]]);
/* Construct NP tetrad for our frame, compute Weyl spinors and Petrov type */
nptetrad(true);
weyl(false);
psi(true);
factor(psi[0]);
factor(psi[1]);
factor(psi[2]);
factor(psi[3]);
factor(psi[4]);
petrov();

To find a Penrose chart for the Taub type D vacuum, first find a transformation to the Taub chart
[tex]
ds^2 = \zeta^{-1/4} \; \left( -d\tau^2 + d\zeta^2 \right)
+ \sqrt{\zeta} \; \left( dx^2 + dy^2 \right)
[/tex]
Then put
[tex]
u = \frac{\tau + \zeta}{\sqrt{2}}, \;
v = \frac{\tau - \zeta}{\sqrt{2}}
[/tex]
and then
[tex]
p = \operatorname{arctan}(u), \;
q = \operatorname{arctan}(v)
[/tex]
The new coordinates are restricted to
[tex]
-\pi/2 < p < q < \pi/2
[/tex]
and give the picture sketched below.

There have been a surprising number of (mostly bad) papers arguing over whether or not a plane symmetric vacuum solution is possible in gtr. Unfortunately, Maxima's Ctensor package is not yet sophisticated enough to compute the acceleration vector associated with the given frames, which would indicate one possibly surprising distinction between these two type D vacuum solutions: while the mass of the Kasner dust from which we obtained the Kasner vacuum as a limiting case is (as we would expect) positive, the mass of the alleged "planar object" at z=0 in the Taub vacuum is negative. It is a good exercise to compute by hand the acceleration [itex]\nabla_{\vec{e}_1} \vec{e}_1[/itex] of the static observer whose world line is an integral curve of [itex]\vec{e}_1 = z^{1/3} \; \partial_t [/itex]. Another good exercise: study the timelike geodesics using the method of effective potentials and notice that the world line of a positive mass test particle is "repelled" from z=0.

(The short answer to the question of whether gtr admits a plane symmetric vacuum is that gtr does not admit models in which the source of the gravitational field is an infinite thin planar sheet with uniform and positive mass density, which is what most writers have in mind when they speak of "plane symmetric vacuum". Since gtr is more realistic theory than Newtonian gravitation, it should not be too shocking that it does not admit certain idealizations which are admissible in Newtonian gravitation!)

To avoid possible confusion: earlier I mentioned the Taub-NUT vacuum, which incorporates a region corresponding to a local vacuum solution which is also called "the Taub vacuum", but which should not be confused with the plane symmetric static vacuum discussed here. The vacuum discussed here has a cuvature singularity at z=0; the Taub region in the Taub-NUT vacuum is singularity-free (indeed, "the" maximal analytical extension of this region, theTaub-NUT vacuum, is singularity-free).

For more information, see Griffiths and Plebanski, section 9.1.2 (for the Petrov D static Taub vacuum) and section 12.1.2 (for the Taub regions in the Taub-Nut vacuum).

Figure:

• Conformal structure of the Kasner dynamical type D vacuum (left) and Taub static type D vacuum (right).

Remember: in this figure, points correspond to euclidean two-planes, not to Riemannian two-spheres.

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VIII. Plane-Sym Spacetimes (cont'd)

You might have noticed that in the previous post, I was cheating just a bit: I was looking at line elements having the form of a direct product of a two-dimensional Lorentzian manifold (signature -+) with a two-dimensional Riemannian manifold, and I simply ignored the second factor. That makes it much easier to find a transformation bringing the metric of the first factor into a form in which, as expressed in the new chart, the line element is conformal to some simple and familiar manifold.

In contrast, recall that in the construction of the standard conformal compactification of Minkowski spacetime in a preceding post in this thread, we found a conformal mapping of Minkowski vacuum into a certain compact region in the Einstein lambdadust, a static spacetime which as a topological manifold is homeomorphic to [itex]R \times S^3[/itex]. Then the fact that the conformal factor blows up on the boundary of this region shows that Minkowski spacetime is inextensible--- it cannot be further extended.

As an example of a more careful construction of a conformal mapping of a plane symmetric spacetime to a region of a spacetime whose causual structure is well understood, specifically the Einstein static lambdadust, let us consider one of the most physically significant of all simple exact solutions of the EFE, the SG16 uniform null dust, which in the Brinkmann chart (1921) is
[tex]
\begin{array}{rcl}
ds^2 & = &
-\mu^2 \, (X^2 + Y^2) \, dU^2 - 2 \, dU \, dV + dX^2 + dY^2 \\
&& -\infty < U, \, V, \, X, \, Y < \infty
[/tex]
where [itex]\mu[/itex] is a real constant closely related to the energy density of the wave. Equivalently, the metric tensor can be written as
[tex]
g = -\sigma^1 \otimes \sigma^1
+ \sigma^2 \otimes \sigma^2
+ \sigma^3 \otimes \sigma^3
+ \sigma^4 \otimes \sigma^4
[/tex]
where the Brinkmann coframe field is
[tex]
\begin{array}{rcl}
\sigma^1 & =&
\frac{-1}{\sqrt{2}} \; \left(
\left( 1 + q^2 \; (X^2+Y^2)/2 \right) \; dU + dV \right) \\
\sigma^2 & =&
\frac{-1}{\sqrt{2}} \; \left(
\left( 1 - q^2 \; (X^2+Y^2)/2 \right) \; dU - dV \right) \\
\sigma^3 & = & dX \\
\sigma^4 & = & dY
\end{array}
[/tex]

Terminological note: "SG16" refers to the fact that this is the 16th item in the classification by Sippel and Goenner of the possible Lie algebras of Killing vector fields of the pp-wave spacetimes. To avoid possible confusion, I should mention that there are a number of classes of exact waves often encountered in the literature on exact solutions of the EFE. Here is a brief overview:

• Kundt waves are more general than pp-waves; in general they are null dust solutions containing a mixture of gravitational and non-gravitational massless radiation,
• vacuum Kundt waves model purely gravitational waves; they are Petrov type III; the tidal tensor (wrt some family inertial observers) includes "shearing terms" (see D'Inverno's textbook for a sketchy discussion of this),
• in general, a pp-wave has a one-dimensional Lie algebra of Killing vector fields, so that its self-isometry group is a one dimensional Lie group of Lorentzian isometries; the generator of the Lie algebra can be taken to be the wave vector of the wave,
• vacuum pp-waves model purely gravitational waves and are Petrov type N; the tidal tensor (wrt some family of inertial observers) lacks "shearing terms" and has the "spin-two" form (expansion along on direction, contraction along another) which is expected from linearized gtr,
• plane waves are a subclass of pp-waves; their Lie algebra of Killing vector fields is at least five dimensional and the wavefronts are "planar" in the sense that they are homogeneous wrt translations within each wavefront; in general they contain a mixture of gravitational and non-gravitational radiation,
• the vacuum plane waves contain only gravitational radiation; these are the exact solutions corresponding to the linearized approximations studied in almost every gtr textbook in a chapter on linearized gravitational waves.

In more detail: the general pp-wave spacetime is, in the Brinkmann chart,
[tex]
\begin{array}{rcl}
ds^2 & = &
-h \, dU^2 - 2 \, dU \, dV + dX^2 + dY^2 \\
&& -\infty < U, \, V, \, X, \, Y < \infty
[/tex]
where h is an arbitrary smooth function of U,X,Y. These will generally be "null dust" solutions which model waves containing a mixture of gravitational and other massless radiation (e.g. EM radiation), with all the radiation sharing the same wave vector [itex]\partial_V[/itex]. The case where h is harmonic in X,Y is exactly the case of the vacuum pp-waves, which contain only gravitational radiation.

For generic h (either general null dust or vacuum case) the only Killing vector field (up to a nonzero constant scalar multiple) is the wave vector field [itex]\vec{\xi} = \partial_V[/itex], a null geodesic congruence which--- remarkably enough--- is covariantly constant, [itex]\nabla_{\vec{Z}} \vec{\xi} = 0[/itex] for any vector field [itex]\vec{Z}[/itex], a property which in fact characterizes the pp-wave spacetimes. But some choices of h give more symmetry. Ehlers and Kundt classified the possible symmetries of vacuum pp-waves, and later Sippel and Goenner did the general case.

The SG16 case is one of the most symmetric of all exact solutions of the EFE: it possesses a seven dimensional Lie algebra of Killing vector fields! Physically, it models a "null dust plane wave" with planar wavefronts and uniform energy density [itex]\mu^2/8/\pi[/itex]. In general, null dust solutions model incoherent massless radiation not having an particular frequency or polarization, but in this case we can if we like add an EM vector potential such that this solution solves both the curved spacetime Maxwell equations and the Einstein equation (this is not possible for the general null dust!). For example
[tex]
\vec{A}= -\frac{\mu}{\omega} \,
\cos(\mu \, \omega \, U) \; \partial_X
+ \frac{\mu}{\omega} \,
\sin(\mu \, \omega \, U) \; \partial_Y
[/tex]
gives the exact circularly polarized uniform EM wave in gtr. Alternatively, the exact linearly polarized uniform EM wave is given by the choice of EM potential
[tex]
\vec{A} = \mu \, U \; \partial_X
[/tex]

Terminological note: before adding the EM potential, we are dealing with the SG16 null dust, in which the nature of the massless nongravitational radiation is not specified. After adding a suitable EM potential, we are dealing with the SG16 null electrovacuum, modeling either a linearly or circularly polarized uniform EM wave; here "null" means that the principle Lorentz invariants
[tex]
F_{ab} \; F^{ab}, \; \; F_{ab} {{}^\ast \!F}^{ab}
[/tex]
of the EM field both vanish identically, as must happen for an EM wave.

Early in the history of gtr, in the special case of plane waves, Rosen found a transformation of a portion of the Brinkmann chart into the so-called Rosen chart, which is much easier to understand. In our example, this transformation is
[tex]
\begin{array}{rcl}
u & = & U \\
v & = & V
+ \mu \; \tan(\mu \, U) \; \frac{X^2+Y^2}{2} \\
x & = & X \; \sec(\mu \, U) \\
y & = & Y \; \sec(\mu \, U)
\end{array}
[/tex]
and its inverse transformation is
[tex]
\begin{array}{rcl}
U & = & u \\
V & = & v
- \mu \; \sin(\mu \, u) \; \cos(\mu \, u) \; \frac{x^2+y^2}{2} \\
X & = & x \; \cos(\mu \, u) \\
Y & = & y \; \cos(\mu \, u)
\end{array}
[/tex]
Applying this transformation to the SG16 null dust plane wave written in the Brinkmann chart brings the line element into the form
[tex]
\begin{array}{rcl}
ds^2 & = & -2 \,du \, dv + \cos(\mu \, u)^2 \;
\left( dx^2 + dy^2) \right) \\
&& -\pi/2 < u < \pi/2, \; \; -\infty < v, \, x, \, y < \infty
\end{array}
[/tex]
This has a nice "fringe benefit": the obvious frame field read off the line element is not the original frame field but a new one, the Rosen frame field
[tex]
\begin{array}{rcl}
\vec{e}_1 & = & \frac{1}{\sqrt{2}} \;
\left( \partial_u + \partial_v \right) \\
\vec{e}_2 & = & \frac{1}{\sqrt{2}} \;
\left( -\partial_u + \partial_v \right) \\
\vec{e}_3 & = & \frac{1}{\cos(\mu \, u)} \; \partial_x \\
\vec{e}_4 & = & \frac{1}{\cos(\mu \, u)} \; \partial_y
\end{array}
[/tex]
which is inertial nonspinning.

The Rosen chart covers only the region [itex]\frac{-\pi}{2 \mu} < u < \frac{\pi}{2 \mu}[/itex], which corresponds to the "strip" [itex]\frac{-\pi}{2 \mu} < U < \frac{\pi}{2 \mu}[/itex] in the Brinkmann chart, because of the rather obvious coordinate singularities in the Rosen chart. These have a physical significance: the Rosen observers in a given x,y plane initially isotropically expand, then momentarily "hover", then isotropically contract and form a "caustic" where they momentarily "occupy the same point", so to speak, and where the expansion tensor of the congruence blows up. (As with expansion in FRW models, the caustic does not have a particular location in the x,y plane.) Then the expansion/recontraction cycle repeats, but only one cycle is covered by each Rosen chart.

The "physical reason" for the repeated expansion/recontraction cycles experienced by our family of Rosen observers (recall that they are inertial observers, so no non-gravitational forces act on them) is of course the fact that the EM wave carries mass-energy, and this energy attracts test particles.

Thus, the strip [itex]-\pi/2 < U < \pi/2[/itex] in the Brinkmann chart has a particular physical significance in terms of the Rosen congruence. (As you might have noticed, strictly speaking there are infinitely many Rosen congruences in our SG16 spacetime related by "phase shifts".)

Similar remarks hold, incidently for other plane waves. In particular, the vacuum plane waves include the exact monochromatic gravitational plane wave (the exact solution whose linearized approximation is studied in most gtr textbooks), and in this solution, there is a congruence of Rosen observers who also periodically expand and contract, with the difference that they form geometrically different caustics.

(Since I have previously discussed this in great detail, to avoid possible confusion, I should say that from the point of view of a family of Rosen observers,

• in a model of a uniform EM wave (linearly or circularly polarized wave, SG16 in the classification of Sippel and Goener), the observers in each x,y plane periodically converge isotropically, meet in a "point caustic", then begin a new expansion/recontraction cycle,
• in a model of a uniform linearly polarized gravitational wave (EK11_0 in a suitable extension of the classification of Ehlers and Kundt, which didn't specifically identify all cases), the observers in an x,y plane expand along one direct but periodically converge anisotropically along another, so they periodically meet along a "line caustic", then begin a new expansion/recontraction cycle,
• in a model of a circularly polarized gravitational wave (EK11), well, here I'll just say that's a different case.

Here "point, line" refer temporarily to the picture in "space at a time" (permissible in the first two cases because the congruence of Rosen observers is vorticity-free. In the second case, the "physical reason" for the repeated expansion/recontraction cycles experienced by the Rosen observers is of course the fact that--- although the stress-energy tensor does not account for this!--- the gravitational wave carries energy and this energy attracts test particles. Compare the discussion in MTW of the "background" of a closely related gravitational plane wave.)

Another remarkable property of the SG16 plane wave is that it is a conformally flat spacetime. We know that because its Weyl tensor vanishes identically. (In contrast, the generic pp-wave is Petrov type N.) The property of conformal flatness characterizes the pp-waves which contain no gravitational radiation, incidentally. This property implies that there must a coordinate transformation such that the line element written in the new chart has the factor of a nonzero scalar function (the conformal factor) times a line element we can recognize as the line element of Minkowski spacetime written in some chart.

What might this transformation be? Well, Maldacena noticed (c. 2002) that a transformation which is quite similar to Rosen's transformation does the trick, namely:
[tex]
\begin{array}{rcl}
u & = & \tan(\mu \,U) \\
v & = & V + \mu \, \tan(\mu \, U) \; \frac{X^2+Y^2}{2} \\
x & = & \sqrt{\mu} \, X \, \sec(\mu \, U) \\
y & = & \sqrt{\mu} \, Y \, \sec(\mu \, U)
\end{array}
[/tex]
whose inverse transformation is
[tex]
\begin{array}{rcl}
U & = & \frac{1}{\mu} \; \operatorname{arctan}(u) \\
V & = & v - \frac{u}{1+u^2} \; \frac{x^2+y^2}{2} \\
X & = & \frac{1}{\sqrt{\mu}} \; \frac{x}{1+u^2} \\
Y & = & \frac{1}{\sqrt{\mu}} \; \frac{y}{1+u^2}
\end{array}
[/tex]
when applied to the SG16 plane wave written in the Brinkmann chart brings the "strip" [itex]-\pi/2 < U < \pi/2[/itex] to
[tex]
\begin{array}{rcl}
ds^2 & = & \frac{1}{\mu \,(1+u^2)} \; \left( - 2 \, du \, dv
+ dx^2 + dy^2 \right) \\
&& -\infty < u, \, v, \, x, \, y < \infty
\end{array}
[/tex]
Thus, the null geodesics in the "strip" behave just like null geodesics in the entire Minkowski spacetime.

Now we can conformally map the entire Minkowski spacetime to a diamond-shaped region on the Einstein static lambdadust, corresponding the strip [itex]-\pi/2/\mu < U < \pi/2/\mu[/tex] in the Brinkmann chart. The combined conformal factor blows up on only part of the previous boundary, so if we didn't already know that we can analytically extend the strip, this procedure would have told us that fact. Carrying out the extension in the Einstein static lambdadust, we find that the SG16 uniform conformally flat null dust plane wave is conformal to the entire Einstein static lambdadust with one null curve removed. This appears as a helical curve in the usual depiction of the Einstein static lambdadust with two angular coordinates suppressed as a "cylinder" (see Hawking and Ellis, Large Scale Structure of Space-Time, Cambridge University Press, 1972 for the three dimensional depiction I have in mind, from which it should be obvious which helical curve I have in mind). Every "point" in the diagram represents a round Riemannian two-sphere, except for points on this helical curve, which represent points. See the figure below. (Berenstein and Nastase, hep-th/0205048, offer a badly drawn picture of this null curve drawn on the cylinder; I think it may be clearer to "unwrap" the cylinder as shown in the figure below.) In other words, in this sense, the conformal boundary of the SG16 conformally flat uniform energy density null dust plane wave is one dimensional.

Maldacena's transformation, like Rosen's transformation, has a nice fringe benefit: there is an obvious frame field which we can read off the line element written in the Maldacena chart. Transforming this frame back to the Brinkmann chart, we can write three frame fields in terms of the Brinkmann chart: the original Brinkmann frame, the Rosen frame, and the Maldacena frame. As we saw, the Rosen frame models certain nonspinning inertial observers who experience repeated expansion/recontraction cycles, with this relative motion occurring within planes, and with one cycle just fitting in the strip [itex]-\pi/2/\mu < U < \pi/2/\mu[/itex]; in the Brinkmann chart we can "see" these cycles and the resulting caustics. In contrast, the Maldacena frame models certain noninertial observers who experience isotropic expansion and recollapse, with the relative motion being three-dimensional, and whose entire history fits in [itex]-\pi/2/\mu < U < \pi/2/\mu[/itex]. What is more, all the fields (i.e. the EM field and the Riemann curvature components) tend to zero, as measured by the Maldacena observers, as they approach future conformal infinity. However, their spatial hyperslices are asymptotic to H^3 in this limit.

We have mapped our SG16 solution--- recall this includes the exact uniform EM wave (either linearly or circularly polarized)--- to a non-compact region of the Einstein static lambdadust, so strictly speaking, "conformal compactification" is a misnomer in this case. In any case, the important point here is that the SG16 null dust plane wave lacks any asympotically flat sheet, so we should not be very surprised that its conformal structure turns out to be quite unlike that of Minkowski spacetime. In particular, the "locus at conformal infinity" is two-dimensional for the Minkowski spacetime (and asympototically flat sheets in other spacetimes), but one-dimensional for the SG16 conformally flat uniform energy density plane wave.

It is instructive to briefly review "three levels of accuracy" in gtr in modeling uniform EM waves (linearly or circularly polarized):

• "test field": ignore all gravitational effects entirely and work in Minkowski vacuum; then each integral curve of the wave vector field "begins" at some point on a three dimensional locus ("past conformal infinity", or scri^- in the standard Penrose diagram for Minkowksi vacuum) and "ends" at some point on another three dimensional locus ("future conformal infinity", or scri^+ in the standard Penrose diagram),
• "linearized gtr": ignore all second order gravitational effects; the linearized uniform EM wave solution suggests that inertial observers (Rosen observers) will contract isotropically in the x,y plane due to the gravitational attraction of the energy in the wave, but cannot give the correct global conformal structure,
• the exact uniform EM wave (the SG16 null dust made into a null electrovacuum by adding a suitable EM potential): fully accounts for both EM and gravitational effects, and turns out to have a conformal structure quite different from that of more naive models; each integral curve of the wave vector field begins on a one-dimensional locus ("past conformal infinity") and ends a a point on "another" one-dimensional locus ("future conformal infinity").

Put more pointedly: the global conformal structure of the exact solution, null geodesics issue from a one-dimensional locus of possible "directions plus emission 'times' at past conformal infinity", rather than from a three-dimensional locus of possible "directions plus emission 'times' at past conformal infinity".

In the latter case, we can think of "the sphere at conformal past infinity" persisting over time. In the former case, due to the isotropic nature of the expansion/recontraction cycles noted above, we can say that it is impossible (in the SG16 null dust) to identify a particular "direction at conformal past infinity" from which a given null geodesic "originated".

By now, I hope the reader is eager to compare the above discussion with the case of a linearly polarized uniform gravitational wave. Maybe you can guess the dimension of the locus at "conformal infinity"!

Figure:

• Left: the "strip" [itex]-\pi/2/\mu < U < \pi/2/\mu[/itex] conformally mapped into a "diamond" shaped region in the Einstein static lambdadust; inside the "diamond", the wave vector field goes from lower right to upper left as indicated.
• Right: Rosen observers experience repeated expansion-contraction cycles; I have also sketched (bold) a typical timelike curve, i.e. world line of a typical observer. I recommend thinking of this picture as "the Penrose diagram of the uniform EM wave" (even though this misses some important features); points on the boundary represent points, and points in the interior represent round Riemannian two-spheres having some radius. In contrast, in the Penrose diagram for Minkowski vacuum, points on scri^+ or scri^- represent round two-spheres corresponding to the possible directions.

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VIII. Plane-Sym Spacetimes (cont'd)

For anyone curious about the three frames I discussed for the SG16 uniform EM plane wave, and who use Maxima, here are some Ctensor files which you can run under wxmaxima in batch mode:

The Brinkmann observers in Brinkmann chart:

/* 
SG16 null electrovacuum uniform EM plane wave; 
Brinkmann chart; Brinkmann coframe
Chart defined on
        -infty < U,V,X,Y < infty
*/
load(ctensor);
cframe_flag: true;
ratchristof: true;
ctrgsimp: true;
/* define the dimension */
dim: 4;
/* list the coordinates */
ct_coords: [U,V,X,Y];
/* define background metric */
lfg: ident(4);
lfg[1,1]: -1;
/* define the coframe; only need enter the nonzero components */
fri: zeromatrix(4,4);
fri[1,1]: -1/sqrt(2)*(1+q*(X^2+Y^2)/2);
fri[1,2]: -1/sqrt(2);
fri[2,1]: -1/sqrt(2)*(1-q*(X^2+Y^2)/2);
fri[2,2]:  1/sqrt(2);
fri[3,3]:  1;
fri[4,4]:  1;
/* setup the spacetime definition */
cmetric();
/* compute a matrix whose rows give frame vectors */
fr;
/* metric tensor g_(ab) */
factor(lg);
/* compute g^(ab) */
ug: factor(invert(lg));
christof(false);
/* Compute fully covariant Riemann components R_(mijk) = riem[i,k,j,m] */
lriemann(false);
/* Compute R^(mijk) */
uriemann(false);
/* Compute Ricci componets R_(jk) */
ricci(true);
/* Compute trace of Ricci tensor */
tracer;
/* Compute R^(jk) */
uricci(false);
/* Compute and display MIXED Einstein tensor G^a_b */
/* For (-1,1,1,1) sig Flip sign of top row to get G^(ab) */
einstein(false);
/* Einstein tensor as matrix */
matrix([ein[1,1],ein[1,2],ein[1,3],ein[1,4]],
[ein[2,1],ein[2,2],ein[2,3],ein[2,4]],
[ein[3,1],ein[3,2],ein[3,3],ein[3,4]],
[ein[4,1],ein[4,2],ein[4,3],ein[4,4]]);
/* electroriemann tensor */
matrix([lriem[2,2,1,1], lriem[2,3,1,1],lriem[2,4,1,1]],
[lriem[3,2,1,1],lriem[3,3,1,1],lriem[3,4,1,1]],
[lriem[4,2,1,1],lriem[4,3,1,1],lriem[4,4,1,1]]);
/* magnetoriemann tensor */
matrix([lriem[2,4,3,1],lriem[2,2,4,1],lriem[2,3,2,1]],
[lriem[3,4,3,1],lriem[3,2,4,1],lriem[3,3,2,1]],
[lriem[4,4,3,1],lriem[4,2,4,1],lriem[4,3,2,1]]);
/* Construct NP tetrad for our frame, compute Weyl spinors and Petrov type */
nptetrad(true);
weyl(false);
psi(true);
factor(psi[0]);
factor(psi[1]);
factor(psi[2]);
factor(psi[3]);
factor(psi[4]);
petrov();

The Rosen observers in Brinkmann chart:

/* 
SG16 null electrovacuum uniform EM plane wave; 
Brinkmann chart; Rosen coframe
Chart defined on
        -infty < U,V,X,Y < infty
*/
load(ctensor);
cframe_flag: true;
ratchristof: true;
ctrgsimp: true;
/* define the dimension */
dim: 4;
/* list the coordinates */
ct_coords: [U,V,X,Y];
/* define background metric */
lfg: ident(4);
lfg[1,1]: -1;
/* define the coframe; only need enter the nonzero components */
fri: zeromatrix(4,4);
fri[1,1]: -1/sqrt(2)*(1+q^2/cos(q*U)^2*(X^2+Y^2)/2);
fri[1,2]: -1/sqrt(2);
fri[1,3]: -q*X*tan(q*U)/sqrt(2);
fri[1,4]: -q*Y*tan(q*U)/sqrt(2);
fri[2,1]: -1/sqrt(2)*(1-q^2/cos(q*U)^2*(X^2+Y^2)/2);
fri[2,2]:  1/sqrt(2);
fri[2,3]:  q*X*tan(q*U)/sqrt(2);
fri[2,4]:  q*Y*tan(q*U)/sqrt(2);
fri[3,1]:  q*X*tan(q*U);
fri[3,3]:  1;
fri[4,1]:  q*Y*tan(q*U);
fri[4,4]:  1;
/* setup the spacetime definition */
cmetric();
/* compute a matrix whose rows give frame vectors */
trigsimp(expand(fr));
/* metric tensor g_(ab) */
factor(lg);
/* compute g^(ab) */
ug: factor(invert(lg));
christof(false);
/* Compute fully covariant Riemann components R_(mijk) = riem[i,k,j,m] */
lriemann(false);
/* Compute R^(mijk) */
uriemann(false);
/* Compute Ricci componets R_(jk) */
ricci(true);
/* Compute trace of Ricci tensor */
tracer;
/* Compute R^(jk) */
uricci(false);
/* Compute and display MIXED Einstein tensor G^a_b */
/* For (-1,1,1,1) sig Flip sign of top row to get G^(ab) */
einstein(false);
/* Einstein tensor as matrix */
matrix([ein[1,1],ein[1,2],ein[1,3],ein[1,4]],
[ein[2,1],ein[2,2],ein[2,3],ein[2,4]],
[ein[3,1],ein[3,2],ein[3,3],ein[3,4]],
[ein[4,1],ein[4,2],ein[4,3],ein[4,4]]);
/* electroriemann tensor */
matrix([lriem[2,2,1,1], lriem[2,3,1,1],lriem[2,4,1,1]],
[lriem[3,2,1,1],lriem[3,3,1,1],lriem[3,4,1,1]],
[lriem[4,2,1,1],lriem[4,3,1,1],lriem[4,4,1,1]]);
/* magnetoriemann tensor */
matrix([lriem[2,4,3,1],lriem[2,2,4,1],lriem[2,3,2,1]],
[lriem[3,4,3,1],lriem[3,2,4,1],lriem[3,3,2,1]],
[lriem[4,4,3,1],lriem[4,2,4,1],lriem[4,3,2,1]]);
/* Construct NP tetrad for our frame, compute Weyl spinors and Petrov type */
nptetrad(true);
weyl(false);
psi(true);
factor(psi[0]);
factor(psi[1]);
factor(psi[2]);
factor(psi[3]);
factor(psi[4]);
petrov();

The Maldacena observers in Brinkmann chart:

/* 
SG16 null electrovacuum uniform EM plane wave; 
Brinkmann chart; Maldacena coframe
Chart defined on
        -infty < U,V,X,Y < infty
*/
load(ctensor);
cframe_flag: true;
ratchristof: true;
ctrgsimp: true;
/* define the dimension */
dim: 4;
/* list the coordinates */
ct_coords: [U,V,X,Y];
/* define background metric */
lfg: ident(4);
lfg[1,1]: -1;
/* define the coframe; only need enter the nonzero components */
fri: zeromatrix(4,4);
fri[1,1]: -1/sqrt(2)*sqrt(q)/cos(q*U)*(1+q*(X^2+Y^2)/2);
fri[1,2]: -1/sqrt(2)/sqrt(q)*cos(q*U);
fri[1,3]: -1/sqrt(2)*sqrt(q)*X*sin(q*U);
fri[1,4]: -1/sqrt(2)*sqrt(q)*Y*sin(q*U);
fri[2,1]: -1/sqrt(2)*sqrt(q)/cos(q*U)*(1-q*(X^2+Y^2)/2);
fri[2,2]:  1/sqrt(2)/sqrt(q)*cos(q*U);
fri[2,3]:  1/sqrt(2)*sqrt(q)*X*sin(q*U);
fri[2,4]:  1/sqrt(2)*sqrt(q)*Y*sin(q*U);
fri[3,1]:  q*X*tan(q*U);
fri[3,3]:  1;
fri[4,1]:  q*Y*tan(q*U);
fri[4,4]:  1;
/* setup the spacetime definition */
cmetric();
/* compute a matrix whose rows give frame vectors */
trigsimp(expand(fr));
/* metric tensor g_(ab) */
factor(lg);
/* compute g^(ab) */
ug: factor(invert(lg));
christof(false);
/* Compute fully covariant Riemann components R_(mijk) = riem[i,k,j,m] */
lriemann(false);
/* Compute R^(mijk) */
uriemann(false);
/* Compute Ricci componets R_(jk) */
ricci(true);
/* Compute trace of Ricci tensor */
tracer;
/* Compute R^(jk) */
uricci(false);
/* Compute and display MIXED Einstein tensor G^a_b */
/* For (-1,1,1,1) sig Flip sign of top row to get G^(ab) */
einstein(false);
/* Einstein tensor as matrix */
matrix([ein[1,1],ein[1,2],ein[1,3],ein[1,4]],
[ein[2,1],ein[2,2],ein[2,3],ein[2,4]],
[ein[3,1],ein[3,2],ein[3,3],ein[3,4]],
[ein[4,1],ein[4,2],ein[4,3],ein[4,4]]);
/* electroriemann tensor */
matrix([lriem[2,2,1,1], lriem[2,3,1,1],lriem[2,4,1,1]],
[lriem[3,2,1,1],lriem[3,3,1,1],lriem[3,4,1,1]],
[lriem[4,2,1,1],lriem[4,3,1,1],lriem[4,4,1,1]]);
/* magnetoriemann tensor */
matrix([lriem[2,4,3,1],lriem[2,2,4,1],lriem[2,3,2,1]],
[lriem[3,4,3,1],lriem[3,2,4,1],lriem[3,3,2,1]],
[lriem[4,4,3,1],lriem[4,2,4,1],lriem[4,3,2,1]]);
/* Construct NP tetrad for our frame, compute Weyl spinors and Petrov type */
nptetrad(true);
weyl(false);
psi(true);
factor(psi[0]);
factor(psi[1]);
factor(psi[2]);
factor(psi[3]);
factor(psi[4]);
petrov();

Unfortunately, Maxima's Ctensor is not yet sufficiently powerful to compute the expansion tensor for the congruences defined by the timelike unit vector field in the three frames, but the above batch files will at least verify that these really are coframe fields on the SG16 plane wave, and will also compute the curvature components. For good measure they compute three Newman-Penrose tetrads corresponding to the real frame fields; since our spacetime is conformally flat, the Petrov type should be type O in each case, and it is.

Note that q replaces [itex]\mu[/itex] in the above Ctensor files!

The files display the Einstein tensor as a 4x4 matrix, but don't forget that you must flip the sign of the top row! See "BRS: Using Maxima for GTR Computations"

www.physicsforums.com/showthread.php?t=378991

I probably should have said that we can cut out a "cylinder" from the SG16 null dust and match this to an EK6 vacuum exterior to obtain the well-known Bonnor beam, an exact solution modeling the gravitational field of an intense beam of nongravitational massless radiation whose energy and momentum is confined inside a cylinder.

 

[Chris Hillman]

BRS: Conformal Compactifications of Spacetimes. VIII. Plane-Sym Spacetimes (cont'd)

I am determined not to let this thread be hijacked by the topic of pp-waves (which could easily happen because this class of exact solutions is so important, not only for classical gtr but also for work towards quantum gravity, and because there is so much to say about them), but I do need to make some important further points regarding the SG16 null dust (or null electrovacuum if you choose an EM potential as I described in my Post #14 above).

Recall that in the Maldacena chart the line element reads
[tex]
\begin{array}{rcl}
ds^2 & = & \frac{1}{\mu \, (1+u^2)}
\left( -2 \, du \, dv + dx^2 + dy^2 \right) \\
&& -\infty < u, \, v, \, x, \, y < \infty
\end{array}
[/tex]
But this only covers the "strip" [itex]-\pi/2/\mu < U < \pi/2/\mu[/itex] in the Brinkmann chart, i.e. one expansion-recontraction cycle of a suitable congruence of Rosen observers in our SG16 null dust plane wave. The point is that the Maldacena chart indicates that null geodesics can easily "run off to coordinate infinity" without actually covering the entire "history of a photon". Indeed, when I discussed the Brinkmann chart
[tex]
\begin{array}{rcl}
ds^2 & = &
-\mu^2 \, \left( X^2+Y^2 \right) \, dU^2
-2 \, dU \, dV + dX^2 + dY^2 \\
&& -\infty < U, \, V, \, X, \, Y < \infty
\end{array}
[/tex]
which as we saw contains no curvature singularities, I (deliberately, to make a point) neglected to check that this really is a global chart covering the entire spacetime. To do that, we need to check that the entire history of each geodesic is contained within the domain. As the Maldacena chart shows, we don't know that this is so simply because the infinite range of the four coordinates suggest that it is so! Furthermore, I want to explain why a "Penrose chart" may not always provide the simplest way to understand the geometric behavior of null geodesics--- in this example, at least, we'll see that in some ways the original Brinkmann chart is perfectly adequate for that purpose.

The geodesic equations for the SG16 null dust plane wave in the Brinkmann chart are quite simple
[tex]
\begin{array}{rcl}
0 & = &\ddot{U} \\
0 & = & \ddot{X} + \mu^2 \, X \, \dot{U}^2\\
0 & = & \ddot{Y} + \mu^2 \, Y \, \dot{U}^2
\end{array}
[/tex]
plus an equation for [itex]\ddot{V}[/itex] (a bug in VB is hiding a double dot over the V!) which we won't need. Plugging [itex]\dot{U} = P[/itex] (a bug in VB is hiding a dot over the U!) into the second two shows that geodesics will exhibit harmonic oscillations in the coordinates X,Y. In particular, for geodesics which pass through X=Y=0 (at some U,V values) we can write
[tex]
\begin{array}{rcl}
X & = & A \, \sin(\mu \, P \,s) \\
Y & = & B \, \sin(\mu \, P \,s)
\end{array}
[/tex]
whence
[tex]
\begin{array}{rcl}
\dot{X} & = & \mu \, P \, A \, \cos(\mu \, P \,s)
= \pm \mu \, P \, \sqrt{A^2-X^2} \\
\dot{Y} & = & \mu \, P \, B \, \cos(\mu \, P \,s)
= \pm \mu \, P \, \sqrt{B^2-Y^2}
\end{array}
[/tex]
Then plugging
[tex]
\begin{array}{rcl}
\dot{U} & = & P \\
\dot{X} & = & \pm \mu \, P \, \sqrt{A^2-X^2} \\
\dot{Y} & = & \pm \mu \, P \, \sqrt{B^2-Y^2}
\end{array}
[/tex]
into the line element
[tex]
0 = -\mu^2 \, \left( X^2+Y^2 \right) \, \dot{U}^2
- 2 \, \dot{U} \, \dot{V} + \dot{X}^2 + \dot{Y}^2
[/tex]
gives the first integrals for a null geodesic which passes (at some point in its history) through U=V=0:
[tex]
\begin{array}{rcl}
\dot{U} & = & P \\
\dot{V} & = & \mu^2 \, P \,
\left( \frac{A^2+B^2}{2} - X^2-Y^2 \right) \\
\dot{X} & = & \pm \mu \, P \, \sqrt{A^2-X^2} \\
\dot{Y} & = & \pm \mu \, P \, \sqrt{B^2-Y^2}
\end{array}
[/tex]
Thus, every null geodesic satisfies [itex]|X| \leq A, \; |Y| \leq B[/itex] for some [itex]A, B \geq 0 [/itex].

Furthermore, the first derivatives wrt the affine parameter are bounded, so our geodesics never run off to coordinate infinity in finite affine parameter (which would indicate that part of the boundary is actually, in a suitable sense, "at finite distance"). Thus, the SG16 null dust is indeed a rare example of an exact solution which is free of curvature singularities, because as the affine parameter runs off to plus or minus infinity, no affinely parameterized null geodesic ever encounters any curvature singularities. By the same token, despite the ubiquity of caustics when we consider families of timelike or null geodesics, the Brinkmann chart is a global chart, because it has no coordinate singularities and covers the entire spacetime.

It's tempting to write down a null geodesic congruence from the above first integrals, but due to intersections of the integral curves, that's probably not a good idea; rather one should simply solve the system of first order ODEs for the affinely parameterized null geodesics themselves. This shows that only the integral curves of the wave vector field [itex]\partial_V[/itex] (which is a well defined null geodesic congruence as written!) has the property that they reach [itex]V=\infty[/itex]! In all other cases, U tends to infinity while X,Y remain finite.

This means that in the "Penrose diagram" in my Post #14, all null geodesics (with future pointing tangent vectors) which are not given by the wave vector [itex]\partial_V[/itex] tend to the same point on the Penrose diagram as timelike geodesics! (Confusingly, the Penrose diagram shown in my Post #14 is not compact, and this point lies "at coordinate infinity", to upper right).

In short, both timelike and null geodesics exhibit, in general, "harmonic oscillations" in X,Y. In both cases, the repeated expansion and recontraction cycles are due to the positive energy density at each event in our spacetime. Due to the large symmetry group, this results in families of geodesics exhibiting caustics, but any event lies on such a caustic, so no one event is distinguished.

A similar analysis works for the EK11_0 plus polarized gravitational plane wave, whose element can be written in the Brinkmann chart as
[tex]
\begin{array}{rcl}
ds^2 & = & -\mu^2 \; \left( X^2-Y^2 \right) \; dU^2
- 2 \, dU \, dV + dX^2 +dY^2 \\
&& -\infty < U, \, V \, X, \, Y
\end{array}
[/tex]
with one crucial difference: this time, we have harmonic oscillation in X only; even as a family of timelike or null geodesics repeatedly expands, hovers momentatarily, and reconverges in X, it continues to expand exponentially in Y, so to speak.

I hope that clarifies some of the more mystifying parts of my Post #14 above. Unfortunately, I can't resist muddying the waters again by drawing attention to a remarkably simple coframe field
[tex]
\begin{array}{rcl}
\sigma^1 & = & -dr \\
\sigma^2 & = & \cos(a r) \, dz \\
\sigma^3 & = & dv + dr \\
\sigma^4 & = & \sin(a r) \, d\phi
\end{array}
[/tex]
which defines a spacetime which is locally isometric to our SG16 uniform null dust plane wave; the given chart is a halfnull Hopf toroidal chart in which the line element is
[tex]
\begin{array}{rcl}
ds^2 & = & 2 \, dv \, dr + \cos(a r)^2 \, dz^2
+ dr^2 + \sin(a r)^2 \, d\phi^2 \\
&& -\infty < v < \infty, \; 0 < r < \pi/2/a,
\; -\pi/a < z, \, \phi < \pi/a
\end{array}
[/tex]
This gives exactly the same frame component expressions for the Einstein tensor, electroriemann and magnetoriemann tensors as found above for the SG16 null dust plane wave. (Easily verified with Maxima, for example!) But the observers corresponding to the given coframe, while inertial and having hypersurface orthogonal world lines, have completely different behavior than the Rosen observers. Note that in this chart, the wavefronts correspond to coordinate cylinders r=r_0. The hyperslices are copies of round S^3 with curvature [itex]a^2[/itex], and the surfaces r=_r0 appear as the Hopf tori organized about the great circles r=0 and r=\pi/2, which in stereographic projection can be plotted as the z axis and a unit circle in the plane z=0. Our observers start at one of these Hopf circles and move radially inwards (dot r < 0) to the other Hopf circle, passing (at the speed of light) the various Hopf tori r=r_0 as they fall. Obviously, this only works for one hover to collapse cycle!

The larger point here is that pretty much everything in gtr offers potentially pitfalls, and an inexperienced physicist is particularly likely to fall into one when studying such extremely simple line elements as we have been studying in this post! Also, mechanical appliation of techniques like Penrose diagrams which work well in some examples is no substitute for care and insight when studying new and possibly very simple looking examples.

 

[Chris Hillman]

BRS: Conformal Compactifcations. V. Some Stnry Axisym Exms (cont'd)

For the conformal diagram of the so-called Ellis wormhole (aka Morris-Thorne wormhole), see my Post #6 in "BRS: Static Axisymmetric 'Gravitationless' Massless Scalar Field Solutions"

www.physicsforums.com/showthread.php?t=433793

 

[Chris Hillman]

BRS: Conformal Compactifcations of Spacetimes. II. Minkowski Vacuum cont'd

I should say a bit more about null geodesic congruences in Minkowski vacuum, as represented in the Penrose conformally compactified chart
[tex]
ds^2 = \frac{-dT^2 + dR^2 + \sin(R)^2 \, d\Omega^2}
{(\cos(T)+\cos(R))^2},
\; \; -\pi < T < \pi, \; 0 < R < |T|
[/tex]
(See my Post #2 above.)

The beacon semicongruence from a given event on a given world line consists of the future portions of all affinely parameterized null geodesics issuing from that event; similarly, the signal semicongruence for an event consists of the past portions of all null geodesics converging on that event. These form the generalization to arbitrary Lorentzian manifolds of the set of null generators of the forward light cone and past light cone respectively. (See Hawking & Ellis for this terminology.) Together, they form the beacon congruence (or signal congruence) associated with the event.

If we choose a different world line through E which has a distinct tangent vector at E, we obtain the same congruence of curves, but the affine parameterization will be different due to the fact that these two observers with world lines passing through E have different notions of "spherically expanding from E". In the sequel, for convenience I will suppress this dependence on the tangent vector at E of our emitter/receiver.

Notice that the wavefronts of the beacon congruence contract spherically on the given event E (as depicted in a frame field with timelike unit vector tangent to the world line of the receiver/emitter), and after passing through E they expand spherically.

The null geodesics forming the beacon congruence form a two parameter family of null geodesics parameterized by direction, i.e. two-spherical coordinates, and of course the null geodesic issuing from past null infinity in a particular direction winds up going off to future null infinity in the antipodal direction.

In particular, in Minkowski vacuum, the beacon congruence from the static observer with world line [itex]x=x_0, \; y=y_0, \; z=z_0[/itex] consists of the integral curves of the null geodesic vector field
[tex]
\vec{\ell} = \partial_t +
\frac{(x-x_0) \, \partial_x + (y-y_0) \, \partial_y + (z-z_0) \, \partial_z}
{\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}}
[/tex]
These integral curves can be written as the affinely parameterized null geodesics
[tex]
\begin{array}{rcl}
t & = & t_0 + s \\
x & = & x_0 + s \, \sin(\theta) \, \cos(\phi) \\
y & = & y_0 + s \, \sin(\theta) \, \sin(\phi) \\
z & = & z_0 + s \, \cos(\theta)
\end{array}
[/tex]
(Notice that these all pass through the event [itex]t=t_0, \, x=x_0, \, y=y_0, \, z=z_0[/itex].)

The transformation to the cartesian chart from the Penrose chart (written using polar-spherical-like coordinates) is
[tex]
\begin{array}{rcl}
t & = & \frac{\sin(T)}{\cos(T)+\cos(R)} \\
x & = & \frac{\sin(R) \, \sin(\Theta) \, \cos(\Phi)}{\cos(T)+\cos(R)} \\
y & = & \frac{\sin(R) \, \sin(\Theta) \, \sin(\Phi)}{\cos(T)+\cos(R)} \\
z & = & \frac{\sin(R) \, \cos(\Theta)}{\cos(T)+\cos(R)}
\end{array}
[/tex]
with inverse transformation (bearing in mind that arctan has multiple branches, so that for some values of the input you'll need to subtract [itex]\pi[/itex] to get coordinate values in the required range)
[tex]
\begin{array}{rcl}
T & = & \arctan(t+\sqrt{x^2+y^2+z^2})+\arctan(t-\sqrt{x^2+y^2+z^2}) \\
R & = & \arctan(t+\sqrt{x^2+y^2+z^2})-\arctan(t-\sqrt{x^2+y^2+z^2}) \\
\Theta & = & \arctan(\sqrt{x^2+y^2}/z) \\
\Phi & = & \arctan(y/x)
\end{array}
[/tex]

Transforming the beacon congruence into the Penrose chart description gives (for a typical example) the picture shown below at left. Note these features:

• a unique null geodesic issues from E and eventually reaches R=0, which is merely a coordinate singularity, so the null geodesic can be continued (in the diagram, this looks like a "reflection") as R increases again, until it reaches a point on future null infinity [itex]T=R[/itex]; in the diagram, points represent two-spheres, so you must imagine the geodesic striking a particular point on the indicated two-sphere at future null infinity,
• tracing this same null geodesic backwards in time, we find that it strikes a point on past null infinity (antipodal point on the indicated two sphere at null infinity shown in the diagram, wrt to the point mentioned in the previous item),
• similarly a unique geodesic traced backwards in time from E reaches R=0 and can be continued through this coordinate singularity (again, it appears to be "reflected" in R=0),
• null geodesics issuing in other directions appear to lie "between" these two extremes, and they end up on points with the expected angular coordinates on various two-spheres at future null infinity.

If we take a limit in which we "move E off to infinity", in particular direction, we obtain the plane wave congruence coming from that direction. In particular, taking the limit [itex]z_0-> \infty[/tex] we obtain the null geodesic vector field
[tex]
\vec{k} = \partial_t + \partial_z
[/tex]
whose integral curves are
[tex]
t = t_0 + s, \; x = x_0, \; y = y_0, \; z = z_0 + s
[/tex]
Transforming this into the Penrose chart depiction, we see that we can think of each integral curve belonging to this congruence as issuing from a particular "ideal point" on past null infinity
[tex]
T = \arctan(t_0-z_0) - \pi/2, \;
R = \arctan(t_0-z_0) + \pi/2, \;
\Theta = \pi, \; \Phi = \arctan(y_0/x_0)
[/tex]
and winding up at the ideal point on future null infinity
[tex]
T = \pi/2 + \arctan(t_0-z_0), \;
R = \pi/2 - \arctan(t_0-z_0), \;
\Theta = 0, \; \Phi = \arctan(y_0/x_0)
[/tex]
Moreover, for a given plane wave congruence (associated with a particular direction and its antipodal direction on the unit sphere), for a given t_0 all geodesics issue from the same ideal two-sphere and wind up at the same ideal two-sphere. Contrast this picture with what happens for null geodesics in a beacon congruence for a non-ideal event E, where the endpoints are distributed over different ideal spheres.

Figures: in Minkowski vacuum, in the Penrose chart:

• Beacon congruence, with selected null geodesics shown in cyan, for the event
  [tex]T=-\arctan(2), \; R =\arctan(2), \; \Theta = 0, \; \Phi = 0 [/tex]
  and for the inertial obsrver whose world line is shown green,
• Plane wave congruence [itex]\partial_t + \partial_z[/itex], with selected null geodesics shown in green for [itex]T=-3 \, \pi/4, \; R=\pi/4[/itex] and in cyan for [itex]T=\pi/4, \; R= 3\,\pi/4[/itex]).