- #1
MarkFL
Gold Member
MHB
- 13,288
- 12
Here is the question:
I have posted a link there to this thread so the OP can view my work.
Differential Equations Harvesting of Fish?
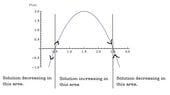
Suppose the growth of the population P=P(t) of a certain fish species in a lake can be modeled by the differential equation dP/dt=kP(1-P/N), where k is the growth rate factor and N is the carrying capacity of the lake. Now, suppose that fishing removes a certain number H of fish per season from the population, then the equation can be modified as dP/dt/kP(1-P/N)-H. The positive constant H is called the harvesting factor.
1. Find the equilibrium points H< kN/4 and show that for any sufficient large initial population Po=P(0), the population of the fish will eventually stabilize at certain level, and this equilibrium level, will decrease gradually to N/2 as the harvesting factor H increases toward kN/4
2. Find the equilibrium points and show that as soon as H>kN/4, regardless how large the initial population Po, all the fish in the lake will be wiped out. Note: You need to show that the rape dP/dt is less than some fixed negative number, so that given enough time, the population will have to decrease to 0.
If you can only help me one of these, i would still greatly appreciate the help!
I have posted a link there to this thread so the OP can view my work.