- #1
Pyrokenesis
- 19
- 0
More "Complex" Complex Analysis
I have another problem that has eluded me for days and I'm sure I'm close. If anyone can help, please nudge me in the right direction.
Consider the mapping w = u + iv = 1/z, where z = x + iy. Show that the region between the curves v = -1 and v = 0 maps into the region outside the circle x^2 + (y - 1/2)^2 = 1/4 and above the line y = 0.
I know that w = x/(x^2 + y^2) + i[-y/(x^2 + y^2)].
I also figured since at v = -1, in the x-y plane, y/(x^2 + y^2) = 1.
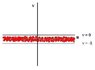
Alas I know not where to go from here. I have attatched a sketch of the region in the v-u plane.
Thanks in advance.
PS: the question then goes on to ask :- What is the image in the x-y plane of the line -1/2? This is obviously a circle since a straight line in one plane is a curve in the other, but how do I prove this?
I have another problem that has eluded me for days and I'm sure I'm close. If anyone can help, please nudge me in the right direction.
Consider the mapping w = u + iv = 1/z, where z = x + iy. Show that the region between the curves v = -1 and v = 0 maps into the region outside the circle x^2 + (y - 1/2)^2 = 1/4 and above the line y = 0.
I know that w = x/(x^2 + y^2) + i[-y/(x^2 + y^2)].
I also figured since at v = -1, in the x-y plane, y/(x^2 + y^2) = 1.
Alas I know not where to go from here. I have attatched a sketch of the region in the v-u plane.
Thanks in advance.
PS: the question then goes on to ask :- What is the image in the x-y plane of the line -1/2? This is obviously a circle since a straight line in one plane is a curve in the other, but how do I prove this?