- #1
altamashghazi
- 43
- 0
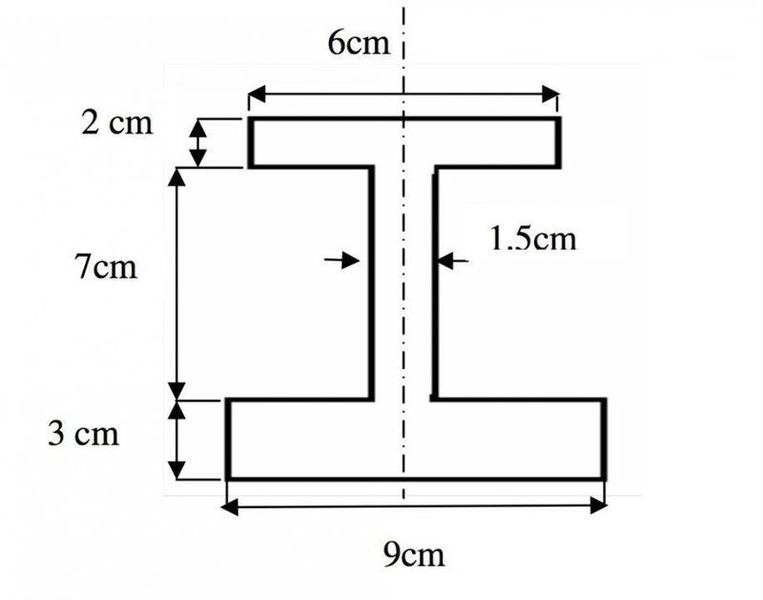
The cross-section of a cost-iron beam is shown in figure below, the loading being in the plane of the web, the upper portion of the section being in compression. If the maximum permissible stresses are 2000 kg/ cm2 in tension and 3000 kg/ cm2 in compression, find the moment of resistance of the section and the actual maximum stresses.