At what angle do we have to kick a ball up the hill for n-rebounds?

[bolzano95]

Homework Statement

Under what angle do we have to kick a ball up the hill so it comes back after n-rebounds?

Relevant Equations

α=?

I decided to try and find a solution in a green (tilted) coordinate system.

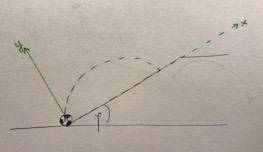
I started solving this problem with thinking about 1-rebound:
##⟹y=0, α=\text{angle under which we kick a ball}##;
##y=sin\alpha v_0t-\frac{1}{2}gt^2##; because I'm trying to solve this in a tilted system, I have to switch to ##g \implies a_y= gcos\varphi##. I get
## 0=sin\alpha v_0t-\frac{1}{2}gcos\varphi t^2##
##\frac{1}{2}gcos\varphi t^2=sin\alpha v_0t##
##\frac{1}{2}gcos\varphi t^2=sin\alpha v_0t \implies sin\alpha = \frac{cos\varphi}{2v_0}tg##

Here I got an angle under which I have to kick a ball for 1-rebound.

But which condition (or more of them) will give me an angle for n-rebounds?
I have been banging my head up the wall for the last few hours, even a relaxing break doesn't help anymore.

Thank you for your help.

 

[haruspex]

Your answer for the 1 rebound case may be "right" (except for a missing factor g at the end), but I don't follow your logic. Anyway, it does not constitute an answer because you have unknowns t and v in there.
Somewhere you should be using the known angle at which the ball must strike the slope, no?
For the n rebound case, consider how the launch angle changes at each bounce.

Edit: I see the missing factor g has been restored.

 

[etotheipi]

I'm likely mistaken, but couldn't we say that if the ball strikes the hill at normal incidence, by symmetry it will bounce back down the hill in exactly the same manner to the starting point?

So if we want ##k## bounces until it reaches its highest point of contact with the hill, where ##v_{\parallel} = 0##, we can write ##v\cos{\alpha} - gt_{k}\sin{\varphi} = 0##. Since each individual bounce lasts ##t_{b} = \frac{2v\sin{\alpha}}{g\cos{\varphi}}##, ##t_{k}## must be an integer multiple, ##k##, of ##t_{b}##? The resulting system when solved should yield a relation only involving angles (the ##v##'s cancel) and then we can substitute in ##n## instead of the integer multiple placeholder (##n=2k-1##)?

 

[haruspex]

if the ball strikes the hill at normal incidence, by symmetry it will back down the hill in exactly the same manner to the starting point?

Quite so, but you should have given @bolzano95 more time to think of that.

For the n bounce case the question is ambiguous. Is it n bounces in total, in which case the out and back paths could be different, or n to the highest point and n-1 returning?

Since each individual bounce lasts ##t_{b} = \frac{2v\sin{\alpha}}{g\cos{\varphi}}##,

Yes, but v and α change at each bounce.

 

[haruspex]

By the way, this can be thought of as purely a problem in algebraic geometry, avoiding any reference to time.

 

[gneill]

I don't believe that the single bounce scenario is viable. The angle of incidence of the ball with the slope is necessarily less that 90° for a parabolic trajectory.

 

[gneill]

Hang on, I was entirely too hasty (read: sloppy) in my thinking:

Clearly it is possible. D'oh!

 

[etotheipi]

Hang on, I was entirely too hasty (read: sloppy) in my thinking:

View attachment 255794

Clearly it is possible. D'oh!

If it makes it any better, I believed you too!

 

[bolzano95]

I'm on to something!

I forgot there is also an acceleration in x-direction as written above. Here is the complete part:
## 0=v_0cos\alpha -gsinφ t ##
## gsinφt=v_0cos\alpha##
##cos\alpha=\frac{gsinφt}{v_0}##
Now, let's express t from condition y=0 (##t=\frac{2sin\alpha v_0}{gcosφ})## and substitute this expression in ##cos\alpha=\frac{gsinφt}{v_0}##. I get the solution as previously indicated: ##tan\alpha=\frac{1}{2tanφ}##.

This is an angle, under which we have to kick a ball for 1-rebound. OK. Now let's go onto n-rebounds.

The ball bounces 2times and it contacts the floors 3x, 3times and with the floors 5x,... you get the idea. Therefore the bounces k are connected with how many times the ball touches the floor and it is truly the way as etotheipi wrote above: ##k=2n-1##.

Now let's say that an individual bounce lasts ##t_b##. So how are k and the bounces connected? ##k=2n-1##.

When I plug this into ##t=kt_b## I get ##t=\frac{n+1}{2}t_b##.

And the final solution would therefore be ##tan\alpha=\frac{1}{tanφ(n+1)}##.

Thank you @etotheipi for clearing the things for me. As you wrote in your post, I totally forgot about x-direction. And then I was stuck. Even in my dreams I wouldn't come with an idea of ##t=kt_b##. But it makes sense. After this I was also stuck on bounces k and n-s. And of course I'm trying to find a solution for n, not k! I didn't even think about bounces and their contact with the floor. After this the transition to final solution was much easier. So thank you again. It really means a lot to me that I solved this with your help.

 

[etotheipi]

And the final solution would therefore be ##tan\alpha=\frac{1}{tanφ(n+1)}##.

That's what I ended up with, though probably best just for completeness to put it in the form ##\alpha = \arctan{\frac{\cot{\varphi}}{(n+1)}}##.

I'd still be interested in trying to work it out geometrically as @haruspex suggested earlier!

 

[haruspex]

That's what I ended up with, though probably best just for completeness to put it in the form ##\alpha = \arctan{\frac{\cot{\varphi}}{(n+1)}}##.

I'd still be interested in trying to work it out geometrically as @haruspex suggested earlier!

We know it describes a parabola. Consider a line at some slope tan(phi) intersecting a parabola y=-ax² at x=+c and x=-d. Write down expressions for the tangents at the points of intersection and for the slope of the line in terms of a, c, d.
What relationship do you get between the three slopes?

And well done to both of you,