- #1
beansbaxter
- 4
- 0
I am not getting anywhere on this one. Here is the problem at hand:
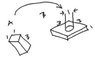
Let's say there are two SOLID objects, both made of the same material... (let's say iron).
The first object (A) is a cuboid that is 3 cm long with sides of 1 cm each.
The second object (B) is a cuboid with sides 3 cm x 3cm and is 1 cm thick.
The latter object (B) has a round hole in the center of it's 3x3 side of 1 cm in diameter.
Calculate the force necessary to insert the first object (A) THROUGH the hole in the second object (B).
I'd like to see the calculations to arrive at the solution as well.
I have attached a pic showing this.
See I am looking for a formula with variables for substituting
a) materials
b) diameters and thicknesses
So that one could have various cuboids of various materials and simply drop them into the equation.
Hope that makes sense.
This is what I have come up with so far:
The calculations would totally depend on the material. It's too dyanamic to calculate manually. If A and B were made of the same materials, both A and B will start to bend. No matter what its made of, the shape of both objects will change if you are using the same materials for both.
It's more than just that, the calculations are literally too complicated to solve analytically, even if you did have all the information. Differential equations can get mighty tricky, mighty fast.
This sort of experiment is best performed rather than modeled.
My first thoughts on this was that the amount of force necessary is all but negligible. (let's call it a net force)
You stand there with your round hole, and wait a while. I'm going to head to the other side of the galaxy and exert an unimaginably small net force on the square peg, causing it to accelerate ever so slightly in the direction of you. A few thousand light years later, I'll have that sucker moving at 90% the speed of light, using a VERY VERY small force.
Hmmmm, on second thought, that might be too fast. I'd be creating black holes and all sorts of the other things that quantum physicists dream about. Note, when the new particle accelerator is completed in 2007, one of the expectations is that by colliding protons and anti-protons, they're hoping to create little tiny black holes...this would be the first analytical evidence in support of string theory.
After those initial thoughts, I thought about it some more and if you're working with more brittle materials, example: a solid piece of chalk, or maybe some ceramic materials, I think you'd only need to know the compressive and sheer strengths of the material.
Then again, I remember one experiment from glass science. We tested the sheer strength of cylindrical glass rods, about 4 cm long, with a diameter of perhaps 1/2 a cm. I recall that there was a HUGE variation in the strengths of the rods. Those who held them in their hands longer had introduced a lot of surface scratches and etching from the pH of their sweat in their hands. So, not only the material is going to come into play, but also the manufacturing process for that material, the microstructure of the material, and surface defects. That ought to make it way too difficult right there. I think the best you could do, even experimentally, is come up with a reasonable range of values, rather than an actual value. And, that range may be small or large, depending on the material used.
Here are some responses by the prof:
I know you'll have to force it, and I also understand that one or the other or both of the objects would experience some deflection. If you need to substitute a material you have more data about, that's cool; I just picked Iron just because.
I don't believe both objects would "bend"... let's say object b was 200 cm thick, but keep the rest of the dimensions for both the same. Object A would perhaps deform uniformly and the take on the shape of the round hole? in otherwords it would become a cyclinder, displacing it's corner mass to the sides? Hmmm... I suppose the first thing we need to do is calculate the volume of the hole in object B and the volume of A.
What would happen if object A was left as it is,l but object B was only 2 mm thick? Would object A remain "square" and the hole would become a square?
Let's say there are two SOLID objects, both made of the same material... (let's say iron).
The first object (A) is a cuboid that is 3 cm long with sides of 1 cm each.
The second object (B) is a cuboid with sides 3 cm x 3cm and is 1 cm thick.
The latter object (B) has a round hole in the center of it's 3x3 side of 1 cm in diameter.
Calculate the force necessary to insert the first object (A) THROUGH the hole in the second object (B).
I'd like to see the calculations to arrive at the solution as well.
I have attached a pic showing this.
See I am looking for a formula with variables for substituting
a) materials
b) diameters and thicknesses
So that one could have various cuboids of various materials and simply drop them into the equation.
Hope that makes sense.
This is what I have come up with so far:
The calculations would totally depend on the material. It's too dyanamic to calculate manually. If A and B were made of the same materials, both A and B will start to bend. No matter what its made of, the shape of both objects will change if you are using the same materials for both.
It's more than just that, the calculations are literally too complicated to solve analytically, even if you did have all the information. Differential equations can get mighty tricky, mighty fast.
This sort of experiment is best performed rather than modeled.
My first thoughts on this was that the amount of force necessary is all but negligible. (let's call it a net force)
You stand there with your round hole, and wait a while. I'm going to head to the other side of the galaxy and exert an unimaginably small net force on the square peg, causing it to accelerate ever so slightly in the direction of you. A few thousand light years later, I'll have that sucker moving at 90% the speed of light, using a VERY VERY small force.
Hmmmm, on second thought, that might be too fast. I'd be creating black holes and all sorts of the other things that quantum physicists dream about. Note, when the new particle accelerator is completed in 2007, one of the expectations is that by colliding protons and anti-protons, they're hoping to create little tiny black holes...this would be the first analytical evidence in support of string theory.
After those initial thoughts, I thought about it some more and if you're working with more brittle materials, example: a solid piece of chalk, or maybe some ceramic materials, I think you'd only need to know the compressive and sheer strengths of the material.
Then again, I remember one experiment from glass science. We tested the sheer strength of cylindrical glass rods, about 4 cm long, with a diameter of perhaps 1/2 a cm. I recall that there was a HUGE variation in the strengths of the rods. Those who held them in their hands longer had introduced a lot of surface scratches and etching from the pH of their sweat in their hands. So, not only the material is going to come into play, but also the manufacturing process for that material, the microstructure of the material, and surface defects. That ought to make it way too difficult right there. I think the best you could do, even experimentally, is come up with a reasonable range of values, rather than an actual value. And, that range may be small or large, depending on the material used.
Here are some responses by the prof:
I know you'll have to force it, and I also understand that one or the other or both of the objects would experience some deflection. If you need to substitute a material you have more data about, that's cool; I just picked Iron just because.
I don't believe both objects would "bend"... let's say object b was 200 cm thick, but keep the rest of the dimensions for both the same. Object A would perhaps deform uniformly and the take on the shape of the round hole? in otherwords it would become a cyclinder, displacing it's corner mass to the sides? Hmmm... I suppose the first thing we need to do is calculate the volume of the hole in object B and the volume of A.
What would happen if object A was left as it is,l but object B was only 2 mm thick? Would object A remain "square" and the hole would become a square?