- #1
Math Amateur
Gold Member
MHB
- 3,990
- 48
I am reading Chapter 3: Jordan Measure ... of Miklos Laczkovich and Vera T Sos's book "Real Analysis: Series, Functions of Several Variables, and Applications" (Springer) ...
I need help with an aspect or step of the proof of Lemma 3.3 ... ...
The statement and proof of Lemma 3.3 of L&S reads as follows:
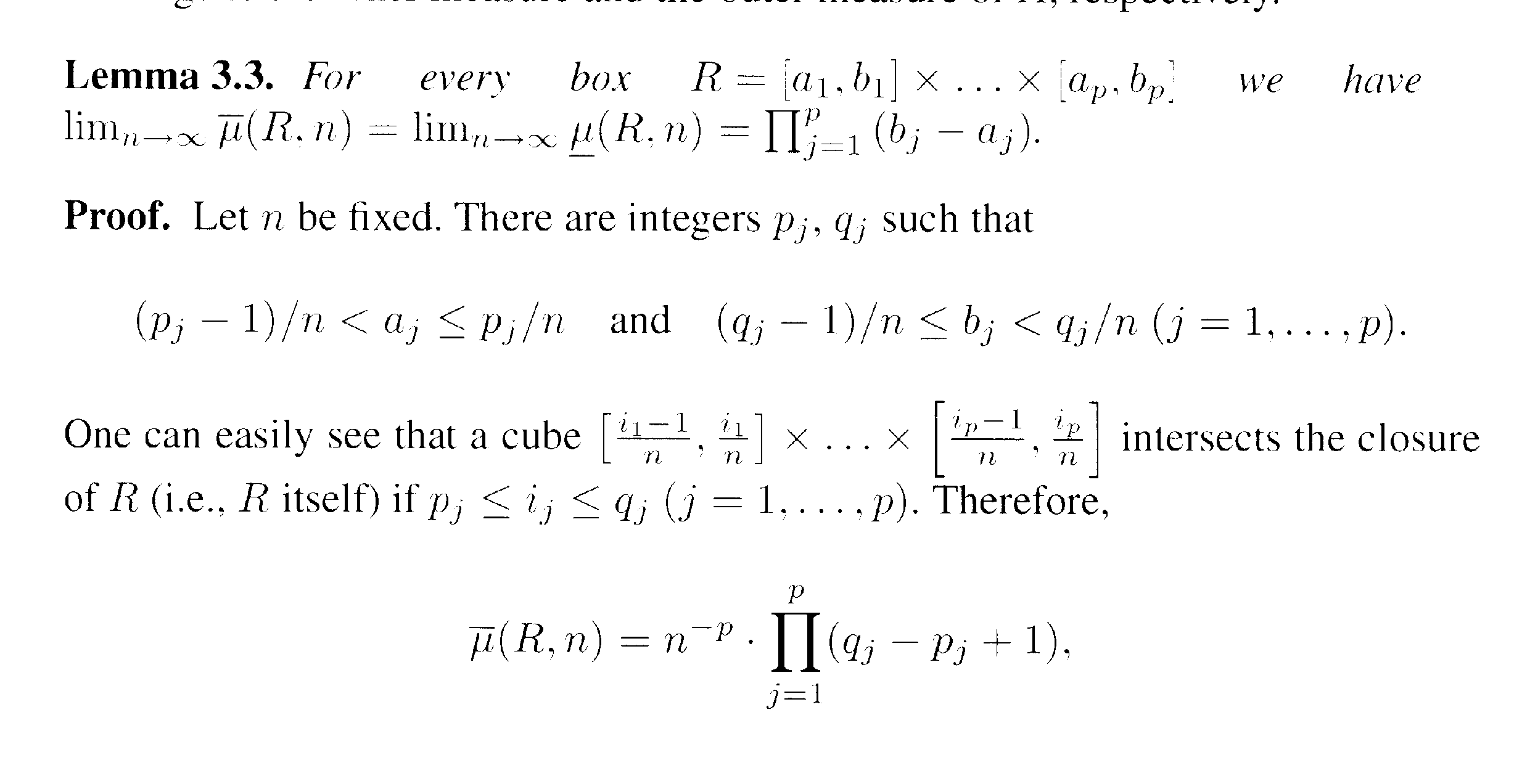
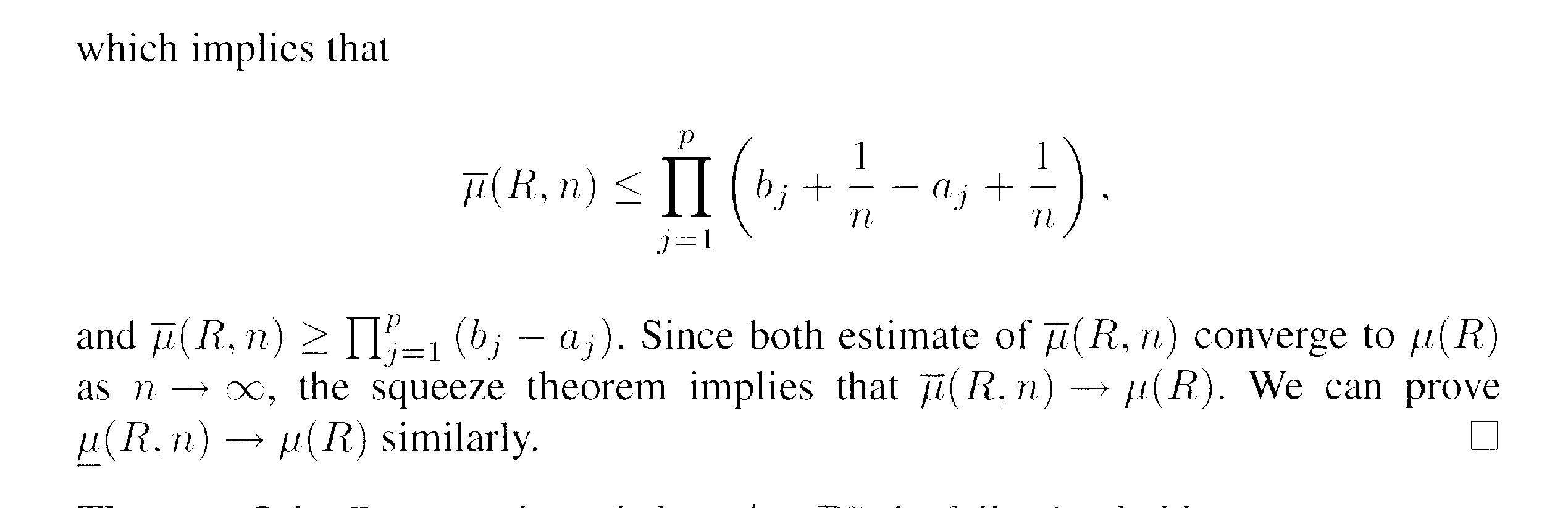
All the necessary definitions together with an explanation of the notation of Lemma 3.3 are given in the scan below ...
In the proof of Lemma 3.3 we read the following:
" ... ... Therefore\(\displaystyle \overline{ \mu } (R,n) = n^{ -p} \prod_{ j =1}^p (q_j - p_j + 1 ) \) ... ... ... "Can someone please help me to prove this ... as yet i have been unable to make a meaningful start on this ...
Help will be appreciated ...
Peter
NOTE:
To make sense of Lemma 3.3 readers of the above post will need access to pages 95-97 of L&S so I providing this text as follows:


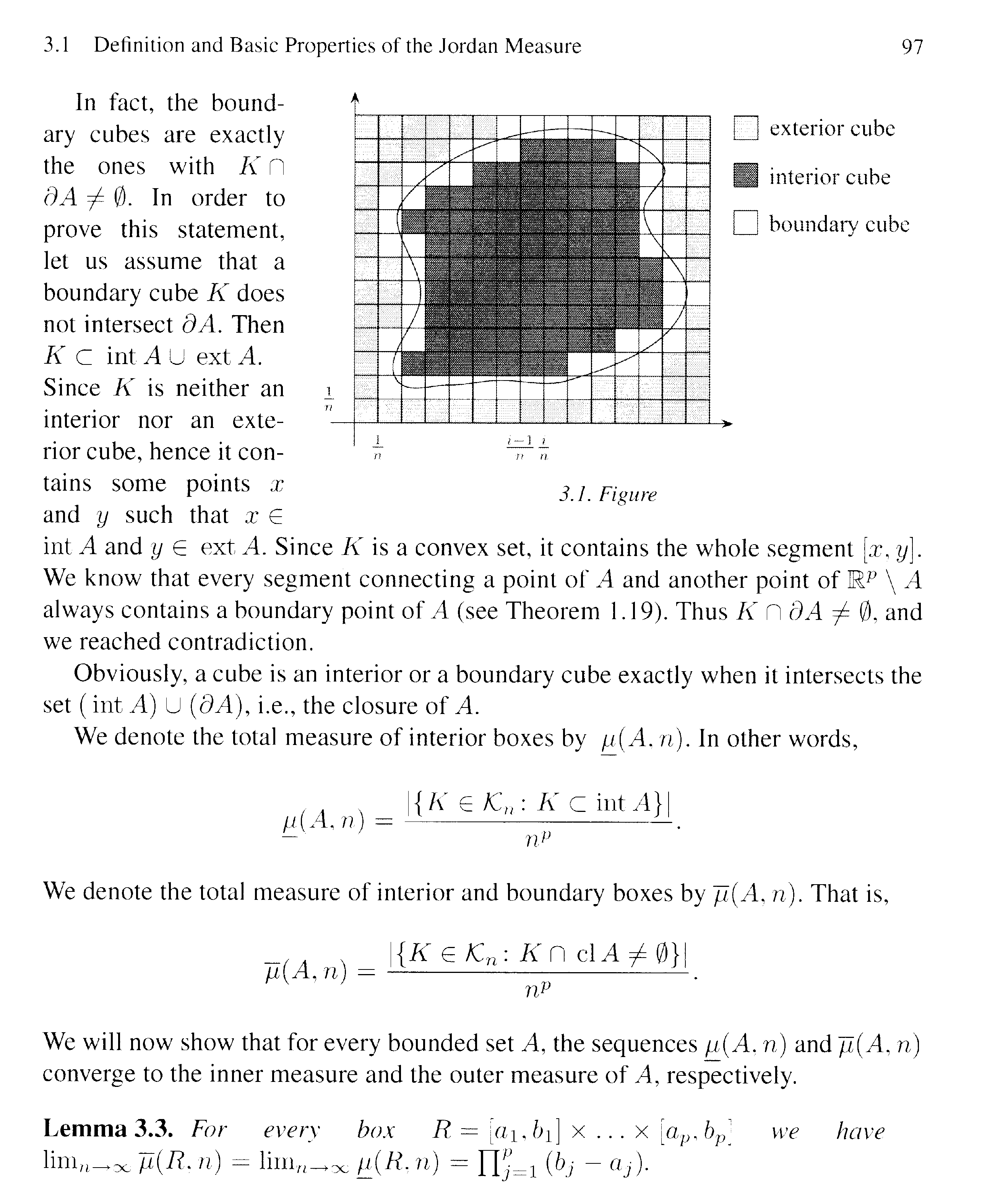
Hope that helps ...Peter
I need help with an aspect or step of the proof of Lemma 3.3 ... ...
The statement and proof of Lemma 3.3 of L&S reads as follows:
All the necessary definitions together with an explanation of the notation of Lemma 3.3 are given in the scan below ...
In the proof of Lemma 3.3 we read the following:
" ... ... Therefore\(\displaystyle \overline{ \mu } (R,n) = n^{ -p} \prod_{ j =1}^p (q_j - p_j + 1 ) \) ... ... ... "Can someone please help me to prove this ... as yet i have been unable to make a meaningful start on this ...
Help will be appreciated ...
Peter
NOTE:
To make sense of Lemma 3.3 readers of the above post will need access to pages 95-97 of L&S so I providing this text as follows:
Hope that helps ...Peter
Last edited: