- #1
arpon
- 235
- 16
Are the accelaration and forces in different inertial referance frame equal ?
arpon said:Are the accelaration and forces in different inertial referance frame equal ?
The precise relativistic expression (which is equivalent to Lorentz's) relating force and acceleration for a particle with non-zero rest massmoving in the x direction with velocity v and associated Lorentz factor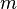 is
is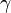
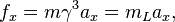
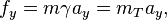
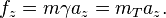
arpon said:Are the accelaration and forces in different inertial referance frame equal ?
Is there any straight forward way to prove these equations by using special relativity ?pervect said:I'm not sure where the best reference is, Wiki has some discussion of the issues at http://en.wikipedia.org/wiki/Mass_in_special_relativity#Transverse_and_longitudinal_mass
arpon said:Is there any straight forward way to prove these equations by using special relativity ?
Acceleration is a measure of the rate of change of velocity over time. It is typically measured in units of meters per second squared (m/s^2). An object can accelerate by either increasing or decreasing its velocity, or by changing its direction of motion.
A reference frame is a set of coordinates used to describe the motion of an object. It provides a point of reference for measuring the position, velocity, and acceleration of an object. In physics, there are two types of reference frames: inertial and non-inertial.
An inertial reference frame is a reference frame in which Newton's first law of motion holds true. This means that an object at rest will remain at rest, and an object in motion will continue in a straight line at a constant speed, unless acted upon by an external force. In other words, there is no net force acting on an object in an inertial reference frame.
In different inertial reference frames, forces act in the same way. This is known as the principle of relativity, which states that the fundamental laws of physics are the same in all inertial reference frames. However, the observed effects of these forces may appear different due to differences in perspective and relative motion between reference frames.
Acceleration may appear different in different inertial reference frames, but the underlying physical laws remain the same. For example, the acceleration due to gravity is the same for all objects in free fall, regardless of their reference frame. However, the perceived acceleration may vary depending on the observer's frame of reference.