A question regarding conditional probabilities

[Lajka]

Hello,

I'm hoping I'm asking this in the right place. If not, I apologize.
Anyway, I have a dilemma about some basics in probabilty and pattern recognition, and, hopefully, someone can help me.

I'm not sure I understand what class-conditional pdf [tex]f(x|w_{i})[/tex] really means, and it's bothering me. Let me elaborate...

When we use terms such as 'conditional probability pdf and cdf', by that we mean:

where A is some event, a subset of a sample space. This event A must also be the domain of our functions defined above. It's a 'new universe', so to speak, for conditional probability cdfs and pdfs, and they only make sense if we look at them over this event A. For example, if we look at the random variable X with Gaussian distribution, and we denote event A as A={1.5<X<4.5}, then the corresponding conditional probability functions (pdf & cdf) look like

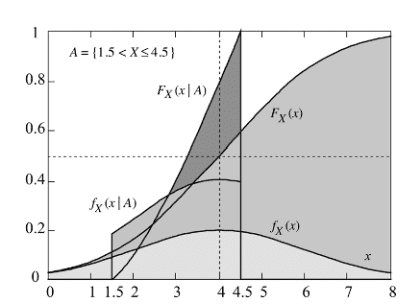
As you can see, they're defined only over interval [tex]{1.5<x<4.5}[/tex], otherwise they wouldn't make sense.
Often we are interested in conditional probabilites functions where the event [tex]A = (Y=y_{0})[/tex], and then we have

[tex]f(x|y)= f(x|Y=y_{0})=f(x,y_{0})/f_{Y}(y_{0})[/tex]

We can interpret function [tex]f(x|y)[/tex] as an intersection of a joint pdf [tex]f(x,y)[/tex] with a plane [tex]y=y_{0}[/tex] (with [tex]f_{Y}(y_{0})[/tex] as a normalization factor).

This is all fairly basic stuff, I reckon. And these types of conditional probability functions are the only types I know that exist, and they're all defined over region which is the event which serves as a condition (I can't stress this enough, for reasons seen later). But class-conditional probability functions, such as [tex]f(x|w_{i})[/tex] in Bayes classifiers theory, seem like a different beast to me.


First of all, let me say that everything about these conditional pdfs, and naive Bayes classifier in general, is perfectly intuitive to me and I don't have a problem from that POV. I understand that, and I don't have the problem with the logic itself presented here. But when I try to define everything rigorously from a mathematical POV, I get stuck.
In other words, I understand what [tex]p(x|w_{i})[/tex] represents, and why, for instance, [tex]p(x|w_{1})[/tex] is non-zero even over region [tex]w_{2}[/tex]. However, I don't know how to explain all that using rigorous mathematical apparatus. Let me elaborate even more...


So, we have these classes [tex]w_{i}[/tex]. What exactly are they, mathematically speaking?! Their priors sum up to one, and they will eventually be represented by regions in our sample space, so I will define them as events in my sample space. If we look at the simplest example in 1-D, the conditional probability density functions would look something like this

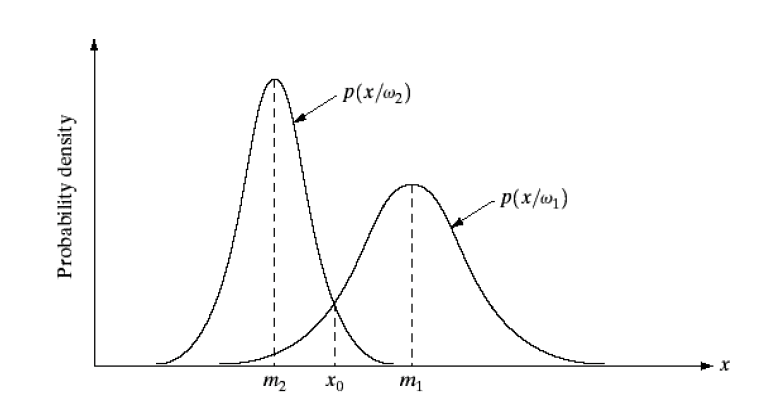
And then we could tell that event [tex]w_{1}[/tex] is [tex](-inf, \, x_{0})[/tex] and event [tex]w_{2}[/tex] is [tex](x_{0},\, +inf)[/tex].

If you ask me, this doesn't make sense if you consider the definitions of conditional pdfs above. Conditional probability density function, by its very definition, must be confined to a space of the event it's conditioned with. In other words, [tex]p(x|w_{1})[/tex] should be constrained to the [tex]w_{1}[/tex] region! But not only that it isn't, it spreads out over the [tex]w_{2}[/tex] region as well! That shouldn't be possible, because [tex]w_{1}[/tex] and [tex]w_{2}[/tex] are mutually exclusive events, and their respective regions also do not overlap, which makes sense. But conditional probability density functions defined over them do? Wait, what?!

Of course, this is how we define the error of our classification, but all this doesn't look very convincing to me, strictly mathematically speaking.
Conditional pdf [tex]p(x|A)[/tex] must be defined over the region which corresponds to the event A, period. Functions [tex]p(x|w_{1})[/tex] and [tex]p(x|w_{2})[/tex] shouldn't overlap each other like that, because the regions [tex]w_{1}[/tex] and [tex]w_{2}[/tex] are mutually exclusive. This is what basic theory of conditional probability density functions tells us.

So, this is why I think that [tex]p(x|w_{i})[/tex] is not an ordinary conditional pdf like the one defined in the beginning of this post. But what is it then?! I don't know, I'm confused. Or maybe I shouldn't interpret classes [tex]w_{i}[/tex] as regions in the sample space, and that's the mistake I'm making here. But what are they then, how should I interpret them?

Also, if I assume that it's okay to interpret classes [tex]w_{i}[/tex] as as regions in space, isn't there a recursive problem, because we first define [tex]p(x|w_{i})[/tex] over, supposedly known, event [tex]w_{i}[/tex], but we actually don't know what region the event [tex]w_{i}[/tex] occupies in sample space? Because, that's, like, the point of classification, to determine these regions, that's what this is all about.
But is this really okay, to define a function in the beginning which domain is actually unknown?

Hopefully, I made at least some sense here, and thanks in advance for any help I can get.
Cheers.

 

[Stephen Tashi]

This is an interesting question! I tend to think of practical problems in verbal terms ( events, statements, information etc.) instead of measure theory terms, so my attempt to explain this may be lacking - which won't deter me from trying!

Suppose we generate a random variable X in by the following process:

We have given two different pdfs [itex] f_1(x) [/itex] and [itex] f_2(x)[/itex]. (Imagine a normal and an exponential pdf, if you like.) We throw a fair die. If the die lands with the 1-face up, we set X equal to a random realization from [itex] f_1 [/itex]. Otherwise we set X equal to a random realization drawn from [itex] f_2 [/itex].

It is possible to define a pdf for X on the real line by [itex] (1/6) f_1(x) + (5/6)f_2(x) [/itex]. However, this is not the most fundamental way to look at the "probability space". The fundamental way to look at it is to look at a pdf whose domain is the space of pairs of numbers (x,k) where x is a real number and k is a integer from 1 to 6. If you look at it that way, then the conditional density of X given that k = 1 is formed by confining our attention to a subset of the domain of the pdf for X.

People who take a practical approach to probabiliy are used to dealing with "point masses". For example, consider an abstract dart game which is scored as follows. For each throw, let R be the distance away from the center of the dartboard that your dart lands. You get 1/R points if your dart lands at a distance more than 3 inches from the center and you get 10 points if your dart lands within 3 inches of the center. If S is the random variable representing a persons score on one dart throw, then a pdf f(s) for S defined on the real numbers would be non-zero on the interval (0,1/3) and at the point s = 10. If you try to do a Riemann integral of such a function, it won't integrate to 1 since the non-zero value f(10) occurs over a point, not over a finite interval. So, from the practical point of view, you declare that the value s = 10 is a "point mass", which means that the type of integration you do, must add the probability that s= 10 to total.

The need for probability theory to deal with a combination of continuous and discrete situations is one of the main motivations for developing advanced theories of integration. You won't be able to visualize the mathematics of such situations by thinking only in terms of Riemann integration.

 

[Lajka]

Hey Stephen, thanks for your answer! I really like this example [itex] f(x,k) = (1/6) f_1(x) + (5/6)f_2(x) [/itex]. But does that mean that we could visualise f(x,k) as

Am I right? Or is this wrong too?
Because I think you're trying to tell me that I'm wasting my time trying to present everything in terms of probability and sample spaces. For example, how would I present [itex]f_1(x)[/itex] here, as a section of [itex]f(x,k)[/itex] and a plane [itex]k=1[/itex]?
However, I think I was wrong now with visualising classes [itex]w_{i}[/itex] as regions, I don't think they are that, regions are just our way of representing classes. That's why there is a room for error, after all. I'm still wrestling with this idea, tho.

Thanks again!

 

[Stephen Tashi]

It is correct to visualize f(x,k) in the coordinate system you illustrated.

how would I present f1(x) here, as a section of f(x,k) and a plane k=1?

Yes, with the understanting that f1 means the density on the condition that k = 1.

I think you're trying to tell me that I'm wasting my time trying to present everything in terms of probability and sample spaces.

No, I don't mean that. In fact, I don't know how you can understand this material in terms other than sample spaces and probability. It s correct to visualize posterior densities as being defined by regions of densities sample spaces. But you can't insist that the sample space always contains each point in the n-dimensional space of real numbers. The sample space might be the cartesian product of a set of the n-dimensional real numbers with a set of discrete things.

Geometric visualization has limited usefulness. You can have complicated conditionals - for example: the conditional density of x given that (x < 2 and the die landed 1) or ( x is between two consecutive odd integers and the die landed 6). I think algebra is a better guide in such situations than geometry.

 

[Lajka]

Yeah, that's my understanding of it now, too. Like I maybe need not force geometric interpretations if algebraic ones seem to be a better fit under the circumstances, like in those examples you mentioned above. But then again, just for the consistency's sake, I like to know that I'm able to do both, if I need to. I'm still wrestling with this, but I think it'll all blend in if I give it time.

Thanks again for all your help!

P.S. Sorry for late responses, I was out of town for the whole week (I was checking forums on my cell, tho).