- #1
Thomas2
- 118
- 0
Note: if you want to avoid opening all the image links below separately, you can go to my webpage http://www.physicsmyths.org.uk/wmap.htm which is essentially identical to this post
The Wilkinson Microwave Anisotropy Probe (WMAP) is a satellite carrying a twin radio telescope for measuring the anisotropy of the Cosmic Microwave Background (CMB) (Fig.1 below) . The particular design of a dual instrument has been chosen in order to reduce the signal noise and therewith effectively increase the sensitivity and stability of the instrument. This is achieved by not measuring the intensity (temperature) of the microwave background for each telescope A and B separately, but only the difference signal I(A)-I(B). If one makes a number of measurements in different directions, the actual intensities can then be retrieved by solving a corresponding set of equations (this yields the sky map shown in Fig.2 ).
Fig.1:
Fig.2:

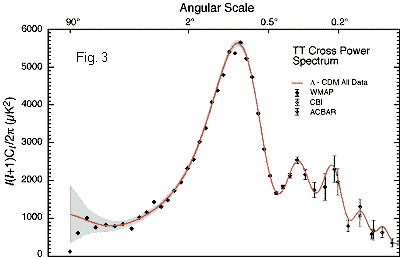
The differential signal itself can be analyzed as well and examined for instance with regard to any non-random features of the fluctuations visible in the sky map. Fig.3 below shows a corresponding spectrum of the scales of the fluctuations in the map, apparently indicating a pronounced peak at 1 deg and a smaller peak at 0.3 deg (the theoretical curve (red) shows further peaks which do however not come out clearly in the data) (see http://map.gsfc.nasa.gov for more information).
Fig.3:
A crucial element in the interpretation of the data is now the beam profile (window function) of the telescope, as it determines the angular resolution of the measurements. NASA quotes the resolution with 0.3 deg (average of V and W bands) which in itself should already raise some suspicion as this is rather close to the features visible in the data. The detailed profile of an individual beam for the individual channels is shown in Fig.4 below (taken from the paper by http://lambda.gsfc.nasa.gov/product/map/pub_papers/firstyear/beams/wmap_window_func.pdf (Fig. 2 there)).
Fig.4:
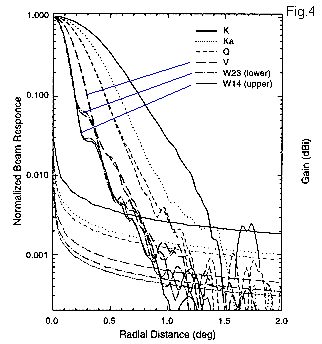
This has been obtained by measuring the transit of a point source (Jupiter) through the beam (for the different channels) and essentially the same profile is also used for the difference signal (Eq.(11) in the paper, which is basically a simple average between the two beams correcting for slight differences between the two channels). However, the cosmic microwave background is essentially uniform and fills the whole beam. Therefore, the difference between the two channels vanishes in zero order and only statistical deviations from this zero signal are being measured. If one assumes that actually a large number N of randomly distributed point sources fills each beam, the statistical variance associated with this is √N. The beam profile for the differential signal is consequently not identical with the profile of the single beam but given by the square root of the latter (i.e. a function exp(-x²) would transform into exp(-0.5x²) ) and the resolution would be only half as good. As a consequence, minor off-center details of the beam profile become suddenly much more pronounced: a portion of the beam with a relative weight of 0.1 in the individual beam has now a weight of √0.1=0.3 for the difference signal (irregularities in the single profile in Fig.4 reach up to a level of 0.1 in the W-channel and, coincidence or not, the ratio of the two main peaks in Fig.3 is about 0.3).
It is therefore likely that the power spectrum (Fig.3), allegedly proving certain features of the Big-Bang Theory, is in fact only an artefact of the data analysis showing features of the beam profile, but has nothing to do with the CMB at all.
By the way, I emailed one of the persons involved with the experiment about this and only got the answer 'I believe we are doing things correctly'.
All images NASA/WMAP Science Team
Note: the above is a copy of my webpage http://www.physicsmyths.org.uk/wmap.htm
The Wilkinson Microwave Anisotropy Probe (WMAP) is a satellite carrying a twin radio telescope for measuring the anisotropy of the Cosmic Microwave Background (CMB) (Fig.1 below) . The particular design of a dual instrument has been chosen in order to reduce the signal noise and therewith effectively increase the sensitivity and stability of the instrument. This is achieved by not measuring the intensity (temperature) of the microwave background for each telescope A and B separately, but only the difference signal I(A)-I(B). If one makes a number of measurements in different directions, the actual intensities can then be retrieved by solving a corresponding set of equations (this yields the sky map shown in Fig.2 ).
Fig.1:
Fig.2:
The differential signal itself can be analyzed as well and examined for instance with regard to any non-random features of the fluctuations visible in the sky map. Fig.3 below shows a corresponding spectrum of the scales of the fluctuations in the map, apparently indicating a pronounced peak at 1 deg and a smaller peak at 0.3 deg (the theoretical curve (red) shows further peaks which do however not come out clearly in the data) (see http://map.gsfc.nasa.gov for more information).
Fig.3:
A crucial element in the interpretation of the data is now the beam profile (window function) of the telescope, as it determines the angular resolution of the measurements. NASA quotes the resolution with 0.3 deg (average of V and W bands) which in itself should already raise some suspicion as this is rather close to the features visible in the data. The detailed profile of an individual beam for the individual channels is shown in Fig.4 below (taken from the paper by http://lambda.gsfc.nasa.gov/product/map/pub_papers/firstyear/beams/wmap_window_func.pdf (Fig. 2 there)).
Fig.4:
This has been obtained by measuring the transit of a point source (Jupiter) through the beam (for the different channels) and essentially the same profile is also used for the difference signal (Eq.(11) in the paper, which is basically a simple average between the two beams correcting for slight differences between the two channels). However, the cosmic microwave background is essentially uniform and fills the whole beam. Therefore, the difference between the two channels vanishes in zero order and only statistical deviations from this zero signal are being measured. If one assumes that actually a large number N of randomly distributed point sources fills each beam, the statistical variance associated with this is √N. The beam profile for the differential signal is consequently not identical with the profile of the single beam but given by the square root of the latter (i.e. a function exp(-x²) would transform into exp(-0.5x²) ) and the resolution would be only half as good. As a consequence, minor off-center details of the beam profile become suddenly much more pronounced: a portion of the beam with a relative weight of 0.1 in the individual beam has now a weight of √0.1=0.3 for the difference signal (irregularities in the single profile in Fig.4 reach up to a level of 0.1 in the W-channel and, coincidence or not, the ratio of the two main peaks in Fig.3 is about 0.3).
It is therefore likely that the power spectrum (Fig.3), allegedly proving certain features of the Big-Bang Theory, is in fact only an artefact of the data analysis showing features of the beam profile, but has nothing to do with the CMB at all.
By the way, I emailed one of the persons involved with the experiment about this and only got the answer 'I believe we are doing things correctly'.
All images NASA/WMAP Science Team
Note: the above is a copy of my webpage http://www.physicsmyths.org.uk/wmap.htm
Attachments
Last edited by a moderator:

