- #1
merzperson
- 32
- 0
1. In case a in the figure block A is accelerated across a frictionless table by a hanging a 10N weight (1.02kg). In case b, block A is accelerated across a frictionless table by a steady 10N tension in the string. The string is massless, and the pulley is massless and frictionless.
Is A's acceleration in case b greater than, less than, or equal to its acceleration in case a?
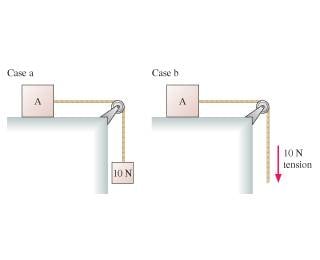
3. I just don't see how a 10N weight differs from a constant 10N downward force on the rope. How is it that the acceleration of block A in case b is greater than in case a? I assume there is some kind of difference because in case a we are comparing two objects and in case b we just calculate the net force on block A, but I can't figure out how to do this.
Is A's acceleration in case b greater than, less than, or equal to its acceleration in case a?
3. I just don't see how a 10N weight differs from a constant 10N downward force on the rope. How is it that the acceleration of block A in case b is greater than in case a? I assume there is some kind of difference because in case a we are comparing two objects and in case b we just calculate the net force on block A, but I can't figure out how to do this.