3D Rigid body dynamics - Rod over rotating disk

[Quesadilla]

Homework Statement

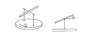
A thin uniform rod is attached to an axis through its midpoint. The axis is standing on a disk rotating with constant angular speed [itex] \Omega [/itex] about its symmetry axis. The rod's midpoint is located directly above the rotational axis of the disk. Let [itex] \theta [/itex] denote the rod's angle with the horizontal plane. Determine how [itex] \theta [/itex] varies with time.

Pictures are attached below to make the above description clearer.

Homework Equations

Tensor of inertia, [itex] I_{\alpha \beta} = \int (r^2 \delta_{\alpha \beta} - r_{\alpha} r_{\beta}) dm [/itex]

Euler's equations for principal systems:

[itex] M_1 = I_{11} \dot{\omega}_1 - \omega_2 \omega_3 (I_{22} - I_{33}) [/itex]
[itex] M_2 = I_{22} \dot{\omega}_2 - \omega_3 \omega_1 (I_{33} - I_{11}) [/itex]
[itex] M_3 = I_{33} \dot{\omega}_3 - \omega_1 \omega_2 (I_{11} - I_{22}) [/itex]

where [itex] M_i [/itex] denotes the components of the net applied moment of force and [itex] \mathbf{\omega} = \omega_1 \mathbf{e}_1 + \omega_2 \mathbf{e}_2 + \omega_3 \mathbf{e}_3 [/itex] is the angular velocity vector, with [itex] \mathbf{e}_i [/itex] being the principal basis vectors.

The Attempt at a Solution

I have tried several things, none of which have yielded satisfactory results. This is amongst the first 3D rigid body dynamics problems I have tried to solve.

Assume an inertial Cartesian coordinate system with the xy-plane coinciding with the horizontal plane of the disk and the z-axis pointing upward perpendicular to this plane. Now introduce an accelerated reference frame constant in the rod. Let the x'-axis be perpendicular to the rod, such that it at a time t=0 is positioned directly above the x-axis with the angle between them being [itex] \theta [/itex]. In the same manner put the y'- and z'-axes, such that they make angles [itex] \theta [/itex] with the y- and z-axis respectively.

In this frame we can write [itex] \Omega \mathbf{e}_z = \Omega \sin \theta \mathbf{e}_{x'} + \Omega \cos \theta \mathbf{e}_{z'} [/itex].

I am not sure how the total angular velocity vector [itex] \omega [/itex] should look like now. I have tried both using the above and adding a term [itex] \dot{\theta} \mathbf{e}_{x'} [/itex] to it. Neither seems to give me a result I want.

Now, I could be wrong but I think this is a principal system, so the tensor of inertia is diagonal and its diagonal elements are given by

[itex] I_{x'x'} = \frac{1}{12} ml^2 [/itex]
[itex] I_{y'y'} = 0 [/itex] (I think, but the value shouldn't matter?)
[itex] I_{z'z'} = \frac{1}{12} ml^2 [/itex]

Euler's equations then gives

[itex] \frac{1}{12} ml^2 (\Omega \cos \theta \dot{\theta}+ \ddot{\theta}) = M_1 = 0. [/itex]

[itex] 0=0 [/itex]

[itex] \frac{1}{12} ml^2 (-\Omega \sin \theta \dot{\theta}) = M_3 = 0. [/itex]

Here I am not happy with what I have got, so I must have gone wrong somewhere in the above. Any hints to where I am messing up are much appreciated. Thank you.

 

[Quesadilla]

I now realize one mistake I made in my original post. The paragraph about the accelerated reference frame introduced makes no sense. The origin 0' is put at the midpoint of the rod, such that the origin remains constant throughout the motion. The x- and x'-axes should coincide, and be perpendicular to rod and parallel to the xy-plane (plane of the disk). The y'- and z'- axes are then tilted an angle [itex] \theta [/itex], such that O'x'y'z' becomes a principal coordinate system for the rod.

Then I think the angular velocity vector [itex] \mathbf{\omega} [/itex] should read something like
[tex] \mathbf{\omega} = \dot{\theta} \mathbf{e}_{x'} + \Omega \sin \theta \mathbf{e}_{y'} + \Omega \cos \theta \mathbf{e}_{z'} [/tex]

Euler's equations then gives

[itex] \frac{1}{12}ml^2 \ddot{\theta} = 0 [/itex]

[itex] 0= 0 [/itex]

[itex] -\frac{1}{12}ml^2 \Omega \dot{\theta} \sin \theta - \frac{1}{12}ml^2 \Omega \dot{\theta} \sin \theta = 0.[/itex]

Maybe there should be an extra minus sign in the last equation, so that the terms will cancel out, but I can't figure out where the mistake is if there is one. Then I get [itex] \ddot{\theta} = 0 [/itex] and I guess [itex] \theta(t) = \dot{\theta}_0 t + \theta_0 [/itex].