- #1
Jazz
- 103
- 5
This is a modified problem from the one posted a few days ago. I’ve been unsuccessfully trying to solve it since then, so maybe it’s time to ask for some help.
I’ve changed the quantities :)
1. Homework Statement
The mass of puck 1 is ##0.2\ kg## and that of puck 2 is ##0.25\ kg##. The initial velocities are ##v_1 = 1.5\ m/s## and ##v_2 = 0.8\ m/s##.
Assuming no friction between the pucks, only normal forces during collision, find their final velocities.
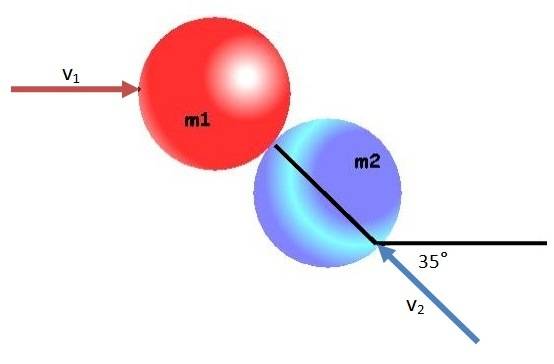
Data:
##m_1 = 0.2\ kg##
##v_1 = 1.5\ m/s##
##m_2 = 0.25\ kg##
##v_2 = 0.8\ m/s##
##\theta: -35º##
##p_{1x} + p_{2x} = p_{1x}’ + p_{2x}’##
##p_{1y} + p_{2y} = p_{1y}’ + p_{2y}’##
##KE_{initial} = KE_{final}##
For a while I thought I was done, but I wasn’t. I’m doing something wrong. Whether is the wrong coordinate system, the signs and/or the math, I don’t know. I appreciate any guidance.
First, I chose a coordinate system so that the line of impact lies along the x-axis. After the collision, one ball will move away from the origin along the line ##y = 0##, while the other will bounce in the sort of wall formed by the y-axis:
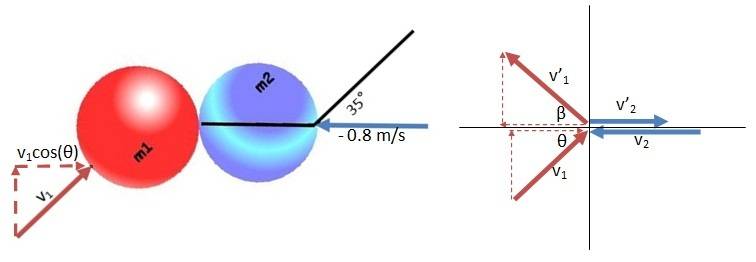
Having established that, ##\theta = 215º##, ##v_2 = -0.8\ m/s## and ##v_2’## will be in the positive direction.
x-axis:
##m_1v_1\cos(\theta) + m_2v_2 = m_1v_1’\cos(\beta) + m_2v_2’##
y-axis:
##m_1v_1\sin(\theta) = m_1v_1’\sin(\beta)##
##v_1\sin(\theta) = v_1’\sin(\beta)##
Conservation of internal KE:
##\frac{1}{2} m_1v_1^2 + \frac{1}{2} m_2v_2^2 = \frac{1}{2} m_1v_1’^2 + \frac{1}{2} m_2v_2’^2##
##m_1v_1^2 + m_2v_2^2 = m_1v_1’^2 + m_2v_2’^2##
Knowing that the overall momentum is conserved ##(p_1 + p_2 = p_1’ + p_2’)##, I used this equation to solve for ##v_2’## and substitute it in the KE equation. Finally, I applied the quadratic formula which gives me the following results:
##v_{1(a)}' = \frac{80+28}{72} = 1.5\ m/s##
##v_{1(b)}' = \frac{80-28}{72} = 0.7\ m/s##
Assuming that ##v_{1(a)}'## is not the answer, being the velocity before the collision, I took ##v_{1(b)}'## as the final velocity. Then, I tried to find ##v_2’##:
##\Delta p_1 = \Delta p_2##
##m_1(v_1’-v_1) = m_2(v_2’-v_2)##
##v_2’ = \frac{m_1(v_1’-v_1)}{m_2}+v_2 = \frac{0.2\ kg (v_1’-1.5\ m/s)}{0.25\ kg}-0.8\ m/s##
If one replaces ##v_1’## by the value obtained in ##v_{1(b)}'##, then ##v_2’## is negative, meaning that ##m_2## is moving in the same direction before the collision (it doesn’t make sense).
If one replaces it by the value obtained in ##v_{1(a)}'##, then ##v_2’## is the same as before the collision ##(-0.8\ m/s)##, meaning that ##m_2## didn’t hit ##m_1## (it doesn’t make sense either).
I haven’t used the equations of momentum along the x or y axis, but I get in trouble when trying to do so. By taking into account that ##v_1\sin(\theta) = v_1’\sin(\beta)##, using the Pythagorean formula/identity and by combining equations I still can’t find a way to reduce the number of unknowns.
Thanks !
I’ve changed the quantities :)
1. Homework Statement
The mass of puck 1 is ##0.2\ kg## and that of puck 2 is ##0.25\ kg##. The initial velocities are ##v_1 = 1.5\ m/s## and ##v_2 = 0.8\ m/s##.
Assuming no friction between the pucks, only normal forces during collision, find their final velocities.
Data:
##m_1 = 0.2\ kg##
##v_1 = 1.5\ m/s##
##m_2 = 0.25\ kg##
##v_2 = 0.8\ m/s##
##\theta: -35º##
Homework Equations
##p_{1x} + p_{2x} = p_{1x}’ + p_{2x}’##
##p_{1y} + p_{2y} = p_{1y}’ + p_{2y}’##
##KE_{initial} = KE_{final}##
The Attempt at a Solution
For a while I thought I was done, but I wasn’t. I’m doing something wrong. Whether is the wrong coordinate system, the signs and/or the math, I don’t know. I appreciate any guidance.
First, I chose a coordinate system so that the line of impact lies along the x-axis. After the collision, one ball will move away from the origin along the line ##y = 0##, while the other will bounce in the sort of wall formed by the y-axis:
Having established that, ##\theta = 215º##, ##v_2 = -0.8\ m/s## and ##v_2’## will be in the positive direction.
x-axis:
##m_1v_1\cos(\theta) + m_2v_2 = m_1v_1’\cos(\beta) + m_2v_2’##
y-axis:
##m_1v_1\sin(\theta) = m_1v_1’\sin(\beta)##
##v_1\sin(\theta) = v_1’\sin(\beta)##
Conservation of internal KE:
##\frac{1}{2} m_1v_1^2 + \frac{1}{2} m_2v_2^2 = \frac{1}{2} m_1v_1’^2 + \frac{1}{2} m_2v_2’^2##
##m_1v_1^2 + m_2v_2^2 = m_1v_1’^2 + m_2v_2’^2##
Knowing that the overall momentum is conserved ##(p_1 + p_2 = p_1’ + p_2’)##, I used this equation to solve for ##v_2’## and substitute it in the KE equation. Finally, I applied the quadratic formula which gives me the following results:
##v_{1(a)}' = \frac{80+28}{72} = 1.5\ m/s##
##v_{1(b)}' = \frac{80-28}{72} = 0.7\ m/s##
Assuming that ##v_{1(a)}'## is not the answer, being the velocity before the collision, I took ##v_{1(b)}'## as the final velocity. Then, I tried to find ##v_2’##:
##\Delta p_1 = \Delta p_2##
##m_1(v_1’-v_1) = m_2(v_2’-v_2)##
##v_2’ = \frac{m_1(v_1’-v_1)}{m_2}+v_2 = \frac{0.2\ kg (v_1’-1.5\ m/s)}{0.25\ kg}-0.8\ m/s##
If one replaces ##v_1’## by the value obtained in ##v_{1(b)}'##, then ##v_2’## is negative, meaning that ##m_2## is moving in the same direction before the collision (it doesn’t make sense).
If one replaces it by the value obtained in ##v_{1(a)}'##, then ##v_2’## is the same as before the collision ##(-0.8\ m/s)##, meaning that ##m_2## didn’t hit ##m_1## (it doesn’t make sense either).
I haven’t used the equations of momentum along the x or y axis, but I get in trouble when trying to do so. By taking into account that ##v_1\sin(\theta) = v_1’\sin(\beta)##, using the Pythagorean formula/identity and by combining equations I still can’t find a way to reduce the number of unknowns.
Thanks !
Last edited: