You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Recent content by Keen94
-
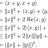
Seeking general advice for geometry
http://www.people.vcu.edu/~rhammack/BookOfProof/ The above link directs you to a book that introduces you to logic and proof writing. Complete Chapter 1: Sets (1.1-1.7) Chapter 2: Logic from Part I. Then skip ahead to Part II- Keen94
- Post #2
- Forum: STEM Academic Advising
-
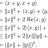
Check my work on these proofs? (basic set theory)
Google: The Book of Proof by Richard Hammack or type in this link http://www.people.vcu.edu/~rhammack/BookOfProof/ Go to Part III section 8. You should be able to find your way a little better.- Keen94
- Post #4
- Forum: Precalculus Mathematics Homework Help
-
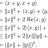
Can Consecutive Powers Be Expressed as Polynomial Formulas?
I edited the post to clear up a few steps.- Keen94
- Post #24
- Forum: Precalculus Mathematics Homework Help
-
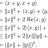
Can Consecutive Powers Be Expressed as Polynomial Formulas?
Let P(p) be the statement ##\sum_{k=1}^{n} k^p= \frac{n^{p+1}}{p+1}\ +An^{p}+Bn^{p-1}+Cn^{p-2}+...## Observe that if p=1, the statement ##\sum_{k=1}^{n} k^1= \frac{n^2}{2}\ +\frac{n}{2}## , is true. Suppose ∀n∈ℤ+, if P(1),...,P(p-1),P(p) are true, then P(p+1). Observe that if p=1,...,p the...- Keen94
- Post #23
- Forum: Precalculus Mathematics Homework Help
-
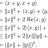
Can Consecutive Powers Be Expressed as Polynomial Formulas?
If you hadn't pointed it out, I would have never noticed. I'll get to it.- Keen94
- Post #22
- Forum: Precalculus Mathematics Homework Help
-
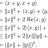
Can Consecutive Powers Be Expressed as Polynomial Formulas?
Would I do the adjusting to the the P(p+1) sum, so that then the P(p) sum is proved?- Keen94
- Post #20
- Forum: Precalculus Mathematics Homework Help
-
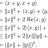
Can Consecutive Powers Be Expressed as Polynomial Formulas?
After adjusting the index of the sum and sending the first term of the sum to the LHS we are left with ##\sum_{k=1}^r k^{p} = \frac{(1+r)^{p+1}}{p+1}+Ar^{p}+Br^{p-1}+Cr^{p-2}+...##- Keen94
- Post #19
- Forum: Precalculus Mathematics Homework Help
-
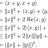
Can Consecutive Powers Be Expressed as Polynomial Formulas?
How hot or cold am I? I'm guessing that the last step is to adjust the index of the the sum on the LHS by subtracting the first term of the sum from both sides.- Keen94
- Post #18
- Forum: Precalculus Mathematics Homework Help
-
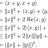
Can Consecutive Powers Be Expressed as Polynomial Formulas?
Since P(k+1) is true whenever P(1),...,P(k) are true then P(k) is true therefore ##\sum_{k=0}^r k^{p} = \frac{(1+r)^{p+1}}{p+1}+Ar^{p}+Br^{p-1}+Cr^{p-2}+...##- Keen94
- Post #16
- Forum: Precalculus Mathematics Homework Help
-
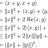
Can Consecutive Powers Be Expressed as Polynomial Formulas?
I suppose it follows that ##(p+2)\sum_{k=0}^r k^{p+1} = (1+r)^{p+2}-1-\left[\sum_{k=0}^r k^0 +(p+2)\sum_{k=0}^{r} k^{1}+...+\frac{(p+2)(p+1)}{2}\ \sum_{k=0}^{r} k^{p}\right]## Then ##\sum_{k=0}^r k^{p+1} = \frac{(1+r)^{p+2}}{p+2}-\frac{1}{p+2}-\frac{1}{p+2}\ \left[\sum_{k=0}^r k^0 +...- Keen94
- Post #14
- Forum: Precalculus Mathematics Homework Help
-
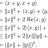
Can Consecutive Powers Be Expressed as Polynomial Formulas?
Let P(p) be the statement ##\sum_{k=1}^n k^p = \frac{n^{p+1}}{p+1}## + polynomial of degree at most p Suppose P(1) is true, we have ##\sum_{k=1}^n k^1=\frac{n^2}{2}+\frac{n}{2}## Suppose ∀n∈ℤ+, if P(1),...,P(p-1),P(p) are all true, then P(p+1) is true. So we have, ##\sum_{k=1}^n...- Keen94
- Post #11
- Forum: Precalculus Mathematics Homework Help
-
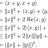
Can Consecutive Powers Be Expressed as Polynomial Formulas?
In other words I just have to get that crucial first term (np+1) / (p+1) and simply reason out that the remaining terms are n's with decreasing power.- Keen94
- Post #10
- Forum: Precalculus Mathematics Homework Help
-
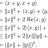
Can Consecutive Powers Be Expressed as Polynomial Formulas?
You're right. Big mistake on my part. What I meant was, am I trying to rewrite my sums so that it fits the definition of the binomial theorem? Therefore I could replace my binomial theorem sums with a polynomial.- Keen94
- Post #7
- Forum: Precalculus Mathematics Homework Help
-
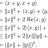
Can Consecutive Powers Be Expressed as Polynomial Formulas?
I think I see it now. Just as (1+K)p+1-kp+1=∑kp then all the other sigmas can be replaced by a polynomial of the form (1+K)n-kn. Is that were you were going with this?- Keen94
- Post #5
- Forum: Precalculus Mathematics Homework Help