- #1
clope023
- 992
- 131
[SOLVED] Work-Energy Theorem
I'm sorry that I do seem to require quite a bit of help, but sometimes when the formulas just aren't working for me I get desperate.
A force is applied to a 2.5kg- radio-controlled model car parallel to the x-axis as it moves along a straight track. The -component of the force varies with the x-coordinate of the car as shown in the figure .Suppose the model car is initially at rest at x=0 and [tex]\vec{F}[/tex] is the net force acting on it.
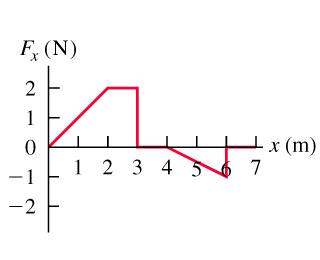
Use the work-energy theorem to find the speed of the car at =3.0.
W = K2-K1
W = Fx
K = 1/2mv^2
(2N)(3m) = 1/2(2.5kg)v^2
6J = 1/2(2.5kg)v^2
12J = 2.5kgv^2
12J/2.5kg = v^2
[tex]\sqrt{12J/2.5kg}[/tex] = v
v = 2.2m/s wrong
another try
W = [tex]\int[/tex]Fx = x^2/2 from x=0 to x = 3
so 9/2 = 1/2(2.5kg)v^2
[tex]\sqrt{9/2.5}[/tex] = v, v= 1.9 wrong
I keep rearranging all the formulas with the information they've given me and still nothing, any help is greatly appreciated.
I'm sorry that I do seem to require quite a bit of help, but sometimes when the formulas just aren't working for me I get desperate.
Homework Statement
A force is applied to a 2.5kg- radio-controlled model car parallel to the x-axis as it moves along a straight track. The -component of the force varies with the x-coordinate of the car as shown in the figure .Suppose the model car is initially at rest at x=0 and [tex]\vec{F}[/tex] is the net force acting on it.
Use the work-energy theorem to find the speed of the car at =3.0.
Homework Equations
W = K2-K1
W = Fx
K = 1/2mv^2
The Attempt at a Solution
(2N)(3m) = 1/2(2.5kg)v^2
6J = 1/2(2.5kg)v^2
12J = 2.5kgv^2
12J/2.5kg = v^2
[tex]\sqrt{12J/2.5kg}[/tex] = v
v = 2.2m/s wrong
another try
W = [tex]\int[/tex]Fx = x^2/2 from x=0 to x = 3
so 9/2 = 1/2(2.5kg)v^2
[tex]\sqrt{9/2.5}[/tex] = v, v= 1.9 wrong
I keep rearranging all the formulas with the information they've given me and still nothing, any help is greatly appreciated.