- #1
Linus Pauling
- 190
- 0
1. Find the sine of the angle between and .
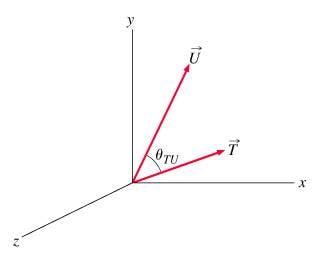
2. AxB = ABsin(alpha)
3. I know T = (3,1,0) and U = (2,4,0), and I calculated that V = TxU = (0,0,10), so the magnitude of V is 10.
Then I did 10 = sqrt(10)*sqrt(20)*sin(alpha)
Divided 10 by sqrt(10)*sqrt(20), took the inverse sine, and obtained 45 degrees, which is incorrect.
2. AxB = ABsin(alpha)
3. I know T = (3,1,0) and U = (2,4,0), and I calculated that V = TxU = (0,0,10), so the magnitude of V is 10.
Then I did 10 = sqrt(10)*sqrt(20)*sin(alpha)
Divided 10 by sqrt(10)*sqrt(20), took the inverse sine, and obtained 45 degrees, which is incorrect.