Understanding the Dirac Delta Identity: A Guide to Fetter and Walecka's Formula

[thatboi]

Hi all,
I'm trying to verify the following formula (from Fetter and Walecka, just below equation (12.38)) but it doesn't quite make sense to me:

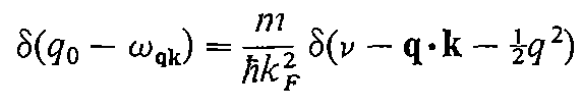
where

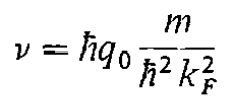and

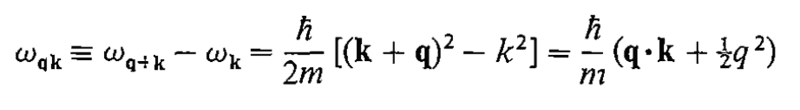
The authors are using the fact that ##\delta(ax) = |a|^{-1}\delta(x)## but to me, it seems like the ##\textbf{q}\cdot\textbf{k}-\frac{1}{2}q^{2}## are missing factors of ##\frac{1}{k_{F}^2}## right?

 

[vanhees71]

From the definition you copied you get
$$q_0=\frac{\hbar k_F^2 \nu}{m}$$ and thus
$$\delta(q_0-\omega_{\boldsymbol{qk}})=\delta \left (\frac{\hbar k_F^2}{m} \nu -\frac{\hbar}{m} (\boldsymbol{q} \cdot \boldsymbol{k} + \frac{1}{2} q^2) \right)=\frac{m}{\hbar k_F^2} \delta \left (\nu- \frac{\boldsymbol{q} \cdot \boldsymbol{k} + q^2/2}{k_F^2} \right).$$

 

[thatboi]

From the definition you copied you get
$$q_0=\frac{\hbar k_F^2 \nu}{m}$$ and thus
$$\delta(q_0-\omega_{\boldsymbol{qk}})=\delta \left (\frac{\hbar k_F^2}{m} \nu -\frac{\hbar}{m} (\boldsymbol{q} \cdot \boldsymbol{k} + \frac{1}{2} q^2) \right)=\frac{m}{\hbar k_F^2} \delta \left (\nu- \frac{\boldsymbol{q} \cdot \boldsymbol{k} + q^2/2}{k_F^2} \right).$$

Ok cool that was what I got as well. Perhaps I missed some other definition along the way.