- #1
amjad-sh
- 246
- 13
While I'm reading a book in quantum mechanics, I reached the part "Generalization to infinite dimension".
We know that at infinite dimension many definitions changes.And that what is confusing me!
Take for example the inner product.when we are dealing in finite dimension the definition of inner product in orthonormal basis is shown below. If we deal with infinite dimensional basis the definition of inner product
becomes as shown below.
My Question is: why we can't use the first definition for infinite dimensional case?What is the magical trick that the first definition makes the inner product equals to infinity while the other makes it equal to a specific number due to the use of integration?Do I need to go deeper in integration theory to grasp this or the idea is simpler than that?
thanks

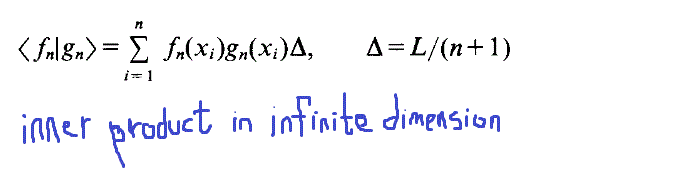
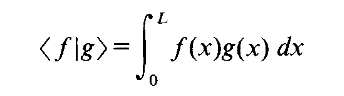
We know that at infinite dimension many definitions changes.And that what is confusing me!
Take for example the inner product.when we are dealing in finite dimension the definition of inner product in orthonormal basis is shown below. If we deal with infinite dimensional basis the definition of inner product
becomes as shown below.
My Question is: why we can't use the first definition for infinite dimensional case?What is the magical trick that the first definition makes the inner product equals to infinity while the other makes it equal to a specific number due to the use of integration?Do I need to go deeper in integration theory to grasp this or the idea is simpler than that?
thanks