- #1
unscientific
- 1,734
- 13
Homework Statement
Homework Equations
The Attempt at a Solution
Not sure what's wrong with mine or the provided solution..both seems to be right.
My Solution:
Provided Solution:
unscientific said:Homework Statement

Homework Equations
The Attempt at a Solution
Not sure what's wrong with mine or the provided solution..both seems to be right.
My Solution:
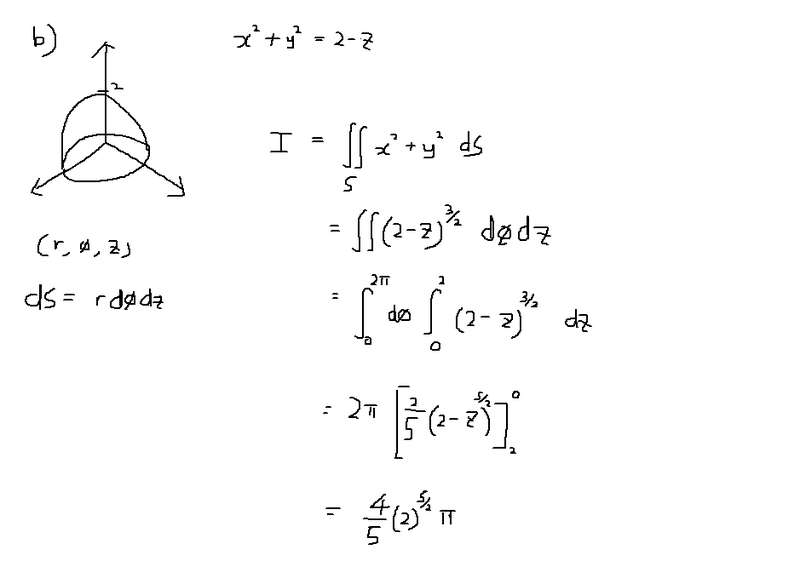
Provided Solution:
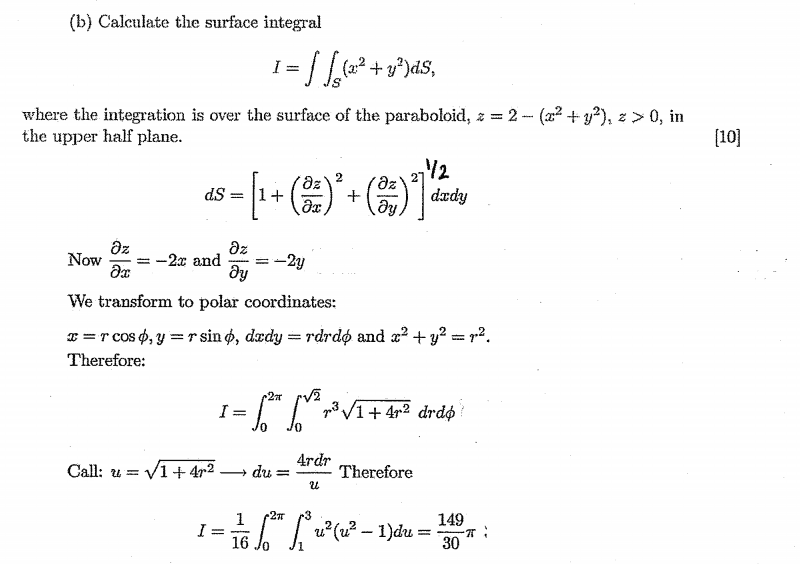
Dick said:I don't know why you just decided to use ##dS=r d\phi dz## instead of calculating it like the book did. Your solution is wrong. The dS you are using looks more like a dS for a cylinder than a paraboloid.
unscientific said:But it shouldn't matter what coordinates you choose, right? It's not exactly a cylinder, as r is changing with z; r = √(2-z) and the equation x2 + y2 = 2 - z
is in the form of x2 + y2 = r2..
LCKurtz said:You must use the correct dS for your parameterization. You can either calculate dS in terms of x and y like they did or directly from your parameterization. The parameterization of that surface in cylindrical coordinates is$$
\vec R(r,\theta)=\langle r\cos\theta,r\sin\theta,2-r^2\rangle$$If you use that approach, the formula for dS is$$
dS = |\vec R_r \times\vec R_\theta|drd\theta$$
unscientific said:Hmm that makes sense. In my geometric derivation of dS, did I assume that R is constant somewhere?
is Rr = ∂R/∂θ
and
Rθ = ∂R/∂r ??
yes, the equation dS=r d(theta) dz only works for a surface of constant (cylindrical) radius. For a general surface, the equation will be different. Also, it doesn't matter which coordinates you use, in the sense that you could useunscientific said:Hmm that makes sense. In my geometric derivation of dS, did I assume that R is constant somewhere?
A surface integral is a mathematical tool used in multivariable calculus to calculate the total value of a three-dimensional surface. It is similar to a regular integral, but instead of integrating over a one-dimensional curve, it integrates over a two-dimensional surface.
A single surface integral calculates the total value of a surface over a single variable, such as area. A double surface integral calculates the total value over two variables, such as volume. It is essentially an extension of the single surface integral, allowing for the calculation of more complex surfaces.
A surface integral is calculated using a double integral, where the first integral represents the area of a small portion of the surface, and the second integral represents the value of the function over that area. This is then summed up over the entire surface to calculate the total value.
Surface integrals have various applications in physics and engineering, such as calculating the flux of a vector field through a surface, finding the center of mass of a three-dimensional object, and calculating the work done by a force on a solid object. They are also used in computer graphics to render three-dimensional images.
To solve a surface integral problem, you first need to determine the bounds of the integral, which will depend on the shape and orientation of the surface. Then, you need to set up the appropriate double integral and evaluate it using techniques such as substitution or integration by parts. It is important to carefully consider the given function and surface to choose the correct method for solving the integral.