- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Solving Equations with Gaussian Elimination: Troubleshooting Mistakes
- Thread starter uzman1243
- Start date
In summary, Gaussian elimination is a method of solving equations by grouping them into smaller sets, then solving one of the smaller sets for a variable in terms of the others.
Physics news on Phys.org
- #2
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,811
- 1,671
uzman1243 said:Homework Statement
When solving 2 equations using gaussian elimination, can we divide one equation by the other?
Can you help me find where I went wrong?
Homework Equations
4x + 2y = 14
2x-y=1
The Attempt at a Solution
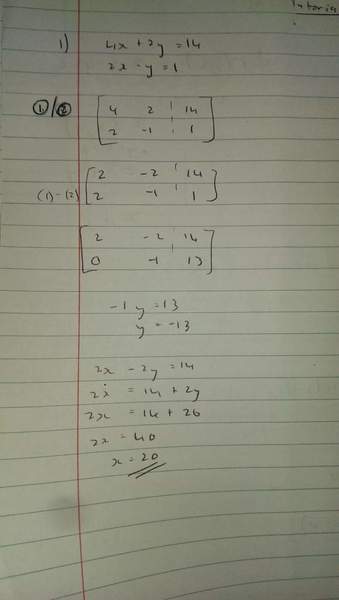
The answer to your question is "Never."
For simple row operations, you are permitted to:
1. Swap two rows with one another.
2. Multiply a row by a non-zero constant.
3. Add one row multiplied by a non-zero constant to another row.
http://en.wikipedia.org/wiki/Gaussian_elimination
And when multiplying a row by a non-zero constant, you must multiply all of the terms in that row (including the right-hand side) by the same non-zero constant.
It appears you have several mistakes in your attached elimination exercise. I would suggest that
you start over from the beginning.
- #3
Ray Vickson
Science Advisor
Homework Helper
Dearly Missed
- 10,704
- 1,722
uzman1243 said:Homework Statement
When solving 2 equations using gaussian elimination, can we divide one equation by the other?
Can you help me find where I went wrong?
Homework Equations
4x + 2y = 14
2x-y=1
The Attempt at a Solution
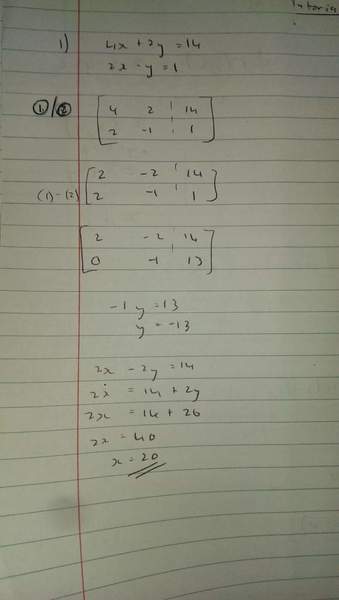
No, you cannot divide equations like that. You can add (or subtract) multiples of one equation onto another, or you can multiply all terms in an equation by a common constant.
So, in the above, you can multiply the second equation by 2 to get 4x - 2y = 2 and then subtract that from the first equation, to get 4x - 4x + 2y + 2y = 14 - 2 --> 4y = 12. Or you can add twice the second equation to the first to get 4x + 2y + 4x - 2y = 14 + 2 --> 8x = 16.
However, fundamentally, what Gaussian elimination is really doing (although it is not always presented as such) is to use one equation to solve for some variable in terms of the others, then to substitute that expression into the other equations, giving a smaller set of equations in which one of the variables has been eliminated. So, we could solve for y from the second equation: y = 2x - 1. Now substitute that into the first equation: 4x + 2(2x-1) = 14, or 8x = 16, as before.
Related to Solving Equations with Gaussian Elimination: Troubleshooting Mistakes
1. What is simple gaussian elimination?
Simple gaussian elimination is a mathematical method used to solve systems of linear equations. It involves transforming a matrix representing the system into an upper triangular matrix through a series of row operations. This process makes it easier to solve the system and find the values of the variables.
2. How does simple gaussian elimination work?
The process of simple gaussian elimination involves dividing the equations in the system into two groups: a leading group and a trailing group. The leading group contains equations with the highest number of variables, while the trailing group contains equations with fewer variables. The goal is to use row operations to eliminate the variables in the trailing group and eventually reduce the system to a triangular form. Finally, the values of the variables can be found by back substitution.
3. When is simple gaussian elimination used?
Simple gaussian elimination is commonly used in engineering, physics, and other scientific fields to solve systems of linear equations. It is particularly useful when dealing with large systems of equations, as it simplifies the process of finding the solution.
4. What are the advantages of using simple gaussian elimination?
One of the main advantages of simple gaussian elimination is that it provides a systematic approach to solving systems of linear equations. It also reduces the amount of time and effort required to find the solution, making it a useful tool for solving complex problems. Additionally, this method is easy to implement and can be used for systems with any number of equations and variables.
5. Are there any limitations to simple gaussian elimination?
Although simple gaussian elimination is a powerful method for solving systems of equations, it does have some limitations. It cannot be used if the matrix representing the system is singular, meaning it has no inverse. Additionally, round-off errors can occur when using this method, which may affect the accuracy of the solution.
Similar threads
-
Precalculus Mathematics Homework Help
- Replies
- 4
- Views
- 2K
-
Precalculus Mathematics Homework Help
- Replies
- 5
- Views
- 2K
-
Precalculus Mathematics Homework Help
- Replies
- 3
- Views
- 1K
-
Precalculus Mathematics Homework Help
- Replies
- 4
- Views
- 2K
-
Calculus and Beyond Homework Help
- Replies
- 7
- Views
- 883
-
Precalculus Mathematics Homework Help
- Replies
- 22
- Views
- 3K
-
Precalculus Mathematics Homework Help
- Replies
- 6
- Views
- 4K
-
Precalculus Mathematics Homework Help
- Replies
- 14
- Views
- 5K
-
Precalculus Mathematics Homework Help
- Replies
- 8
- Views
- 2K
-
Precalculus Mathematics Homework Help
- Replies
- 5
- Views
- 807
Share:
