- #1
paulmdrdo
- 89
- 2
MENTOR NOTE: Moved here from the General Math forum hence no homework template.
Hello! Sorry for not showing what I have tried to solve the problem.
Here it is
I let x = amount of inferior tea to be added to superior tea in lbs.
y = amount of superior tea in lbs.
3x+5y = 11/3(x+y)
solving for x I get x = 2y from here I cannot proceed.
Honestly this is only where I can get to. Please bear with me.
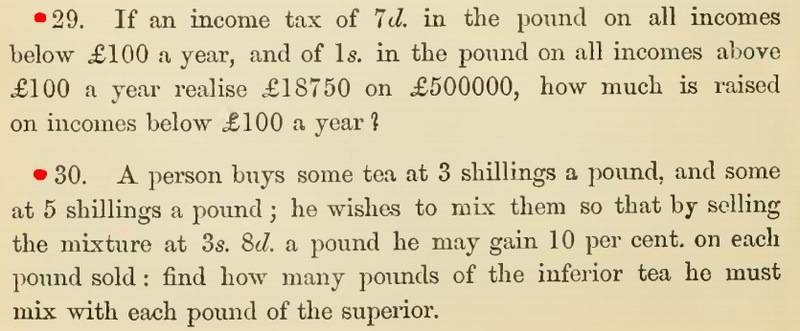
Hello! Sorry for not showing what I have tried to solve the problem.
Here it is
I let x = amount of inferior tea to be added to superior tea in lbs.
y = amount of superior tea in lbs.
3x+5y = 11/3(x+y)
solving for x I get x = 2y from here I cannot proceed.
Honestly this is only where I can get to. Please bear with me.
Last edited by a moderator: