- #1
UMath1
- 361
- 9
I am confused about how the magnetic field of a solenoid is calculated in this image.
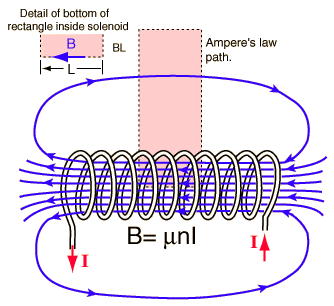
Why is only the current going into the page included in calculating the magnetic field? Shouldn't the field be twice the amount calculated because there is a magnetic field generated by the part of the turns the bottom with current going out of the page? And I don't understand why the vertical components of the path are taken to be zero. Although it is said that the field is perpendicular, the diagram shows that there is a portion of the field parallel to the vertical path.
Why is only the current going into the page included in calculating the magnetic field? Shouldn't the field be twice the amount calculated because there is a magnetic field generated by the part of the turns the bottom with current going out of the page? And I don't understand why the vertical components of the path are taken to be zero. Although it is said that the field is perpendicular, the diagram shows that there is a portion of the field parallel to the vertical path.