- #1
GeoKenshin
- 8
- 0
Hi. I've been having trouble with 2 problems and I've worked them both 2 or 3 times. Here's my problems and my work. Any help will be greatly appreciated.
1.
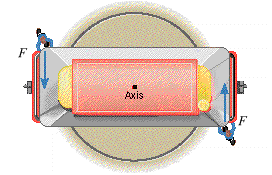
In San Francisco a very simple technique is used to turn around a cable car when it reaches the end of its route. The car rolls onto a turntable, which can rotate about a vertical axis through its center. Then, two people push perpendicularly on the car, one at each end, as in the drawing. The turntable is rotated one-half of a revolution to turn the car around. If the length of the car is 9.80 m and each person pushes with a 185 N force, what is the magnitude of the net torque applied to the car?
T=F (LcosTheta)
I also used the (F1 + F2) L equation but i just got the same answer with a positive sign
T=F (LcosTheta)
T = 370(9.8cos180) = -3626
2.
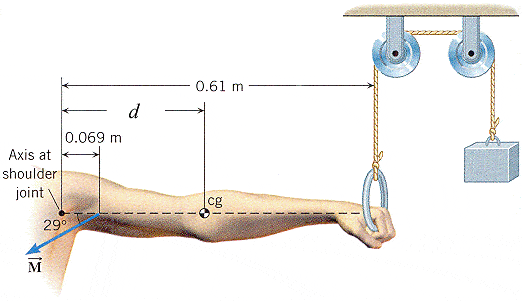
The drawing shows an outstretched arm (0.61 m in length) that is parallel to the floor. The arm is pulling downward against the ring attached to the pulley system, in order to hold the 126 N weight stationary. To pull the arm downward, the latissimus dorsi muscle applies the force vector M in the drawing, at a point that is 0.069 m from the shoulder joint and oriented at an angle of 29°. The arm has a weight of 44 N and a center of gravity (cg) that is located d = 0.26 m from the shoulder joint. Find the magnitude of vector M .
T = -Wa(La) - Wd(Ld) + M (Lm) = 0
I used the above equation to get M = [Na(La/Center of Gravity) + Nb(Lb)]/Lm
[44N(.26m) + 126N(.61m)]/[.69mcos29] = 146.316 N
That Answer isn't right and I'm really stuff on what I could be doing wrong.
Thanks in advance for any assistance.
1.
Homework Statement
In San Francisco a very simple technique is used to turn around a cable car when it reaches the end of its route. The car rolls onto a turntable, which can rotate about a vertical axis through its center. Then, two people push perpendicularly on the car, one at each end, as in the drawing. The turntable is rotated one-half of a revolution to turn the car around. If the length of the car is 9.80 m and each person pushes with a 185 N force, what is the magnitude of the net torque applied to the car?
Homework Equations
T=F (LcosTheta)
The Attempt at a Solution
I also used the (F1 + F2) L equation but i just got the same answer with a positive sign
T=F (LcosTheta)
T = 370(9.8cos180) = -3626
2.
Homework Statement
The drawing shows an outstretched arm (0.61 m in length) that is parallel to the floor. The arm is pulling downward against the ring attached to the pulley system, in order to hold the 126 N weight stationary. To pull the arm downward, the latissimus dorsi muscle applies the force vector M in the drawing, at a point that is 0.069 m from the shoulder joint and oriented at an angle of 29°. The arm has a weight of 44 N and a center of gravity (cg) that is located d = 0.26 m from the shoulder joint. Find the magnitude of vector M .
Homework Equations
T = -Wa(La) - Wd(Ld) + M (Lm) = 0
The Attempt at a Solution
I used the above equation to get M = [Na(La/Center of Gravity) + Nb(Lb)]/Lm
[44N(.26m) + 126N(.61m)]/[.69mcos29] = 146.316 N
That Answer isn't right and I'm really stuff on what I could be doing wrong.
Thanks in advance for any assistance.

