- #1
Permanence
- 53
- 2
Thank you for taking the time to read my thread. I do not agree with the TA's correction of my quiz and would appreciate if someone could give it a look before I approach him about it.
Cobalt-60 has a half-life of 5.24 years. How long would it take for a 100 mg sample of Cobalt-60 to decay to 1 mg?
y = sample*e^(-k*t)
I assumed that k was negative because it was a decay problem. My TA did not agree. I also assumed that the answer must be positive, and it appears that ln(1/100) is indeed negative. We did not have calculators for this quiz.
k = -ln(2) / 5.24
y = 100 * e^-[(ln(2)/5.24)*t]
t = ln(1/100) / [ln(2)/5.24) ; where t is expressed in years
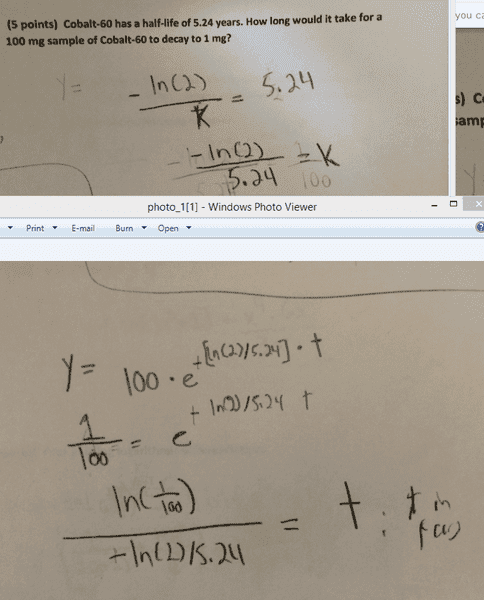
Homework Statement
Cobalt-60 has a half-life of 5.24 years. How long would it take for a 100 mg sample of Cobalt-60 to decay to 1 mg?
Homework Equations
y = sample*e^(-k*t)
I assumed that k was negative because it was a decay problem. My TA did not agree. I also assumed that the answer must be positive, and it appears that ln(1/100) is indeed negative. We did not have calculators for this quiz.
The Attempt at a Solution
k = -ln(2) / 5.24
y = 100 * e^-[(ln(2)/5.24)*t]
t = ln(1/100) / [ln(2)/5.24) ; where t is expressed in years