- #1
Happiness
- 679
- 30
The book argues that since substituting ##\theta## by ##-\theta## leaves the orbit equation (3.34) unchanged, the orbit is therefore invariant under reflection about the apsidal vectors (Fig 3.12).
If substituting ##\theta## by ##-\theta## leaves the orbit equation (3.34) unchanged, then there exists a plane of symmetry (where ##\theta=0##) in the orbit. How does the book reach the conclusion of invariance under reflection about the apsidal vectors?

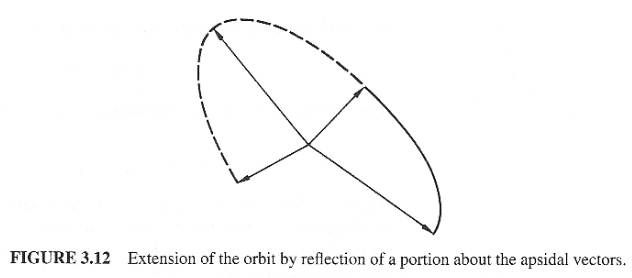
If substituting ##\theta## by ##-\theta## leaves the orbit equation (3.34) unchanged, then there exists a plane of symmetry (where ##\theta=0##) in the orbit. How does the book reach the conclusion of invariance under reflection about the apsidal vectors?