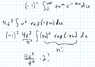- #1
brinraeven
Homework Statement
[/B]
Determine the value that A (assumed real) must have if the wavefunction is to be correctly normalised, i.e. the volume integral of |Ψ|2 over all space is equal to unity.
Homework Equations
Integration by parts
The Attempt at a Solution
So, I've managed to do the integration correctly (I think), but I don't know where to go from here. I have the solution manual, but it skips most steps, so I don't know how to get there. It seems like it has something to do with writing out e^-x as a sum, since factorials play into it, but I don't know how.
My work:
Solution manual: