- #1
chipotleaway
- 174
- 0
Actually, the theorem is that functions that are uniformly continuous are Riemann integrable, but not enough room in the title!
I'm failing to see the motivation behind proof given in my lecturer's notes (page 35, Theorem 3.29) and also do not understand the steps.
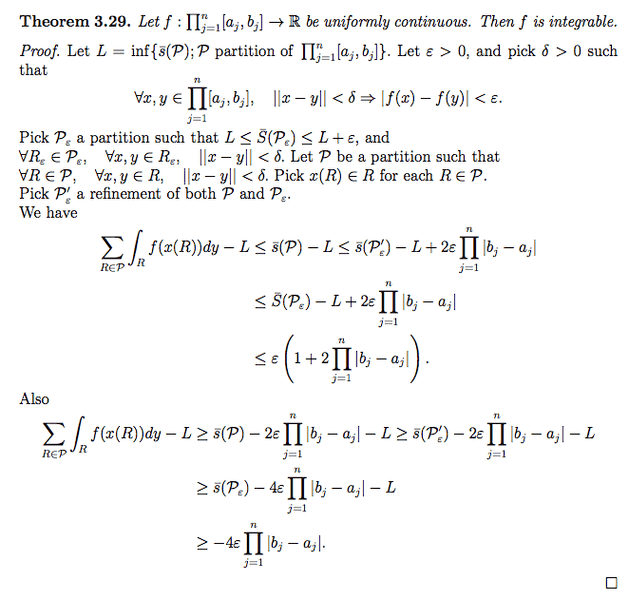
1) First thing I'm not sure I understand is in the first line of the proof - the definition of L. I think this is the set of all upper Riemann sums corresponding to different partitions, because for a given partition P, isn't the upper Riemann sum of f over P unique?
Then taking the infimum of the set would be taking the smallest upper Riemann sum.
2) I have no idea how the chain of inequalities come about, not even the first one.
3) Isn't the proof done by line 3 of the inequalities (before 'Also')? What do the last 3 lines show?
Any help is much appreciated - these proofs are doing my head in.
I'm failing to see the motivation behind proof given in my lecturer's notes (page 35, Theorem 3.29) and also do not understand the steps.
1) First thing I'm not sure I understand is in the first line of the proof - the definition of L. I think this is the set of all upper Riemann sums corresponding to different partitions, because for a given partition P, isn't the upper Riemann sum of f over P unique?
Then taking the infimum of the set would be taking the smallest upper Riemann sum.
2) I have no idea how the chain of inequalities come about, not even the first one.
3) Isn't the proof done by line 3 of the inequalities (before 'Also')? What do the last 3 lines show?
Any help is much appreciated - these proofs are doing my head in.