Natural Frequency Using Rayleighs Energy Method

[j1mb0b]

Hi everybody!

I'm a complete newbie here, but I was hoping somebody might be able to help me out with understanding Rayleighs Energy Method and how to calculate the static deflections/natural frequencies.

I am basically looking for the first and second modes/natural frequencies of a 2 mass shaft supported on 2 bearings situated between the masses. So the masses are overhanging either side of the bearing assemblies. The equivalent diagram that I have assumed is shown below:

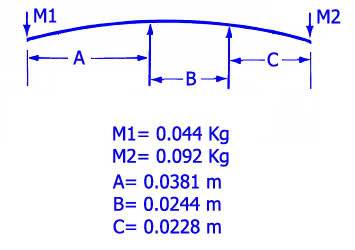
So I have read that Rayleighs Energy Method is a good first approximation for this. I have had a look at it and I can understand how it works, but I can't calculate the deflections due to the masses, as I am not sure of the formula.

Here is a similar system that I have looked at, but unfortunately the formulae are much simpler as the masses/distances are symmetrical...

I have also had a go at doing it using these formulae:

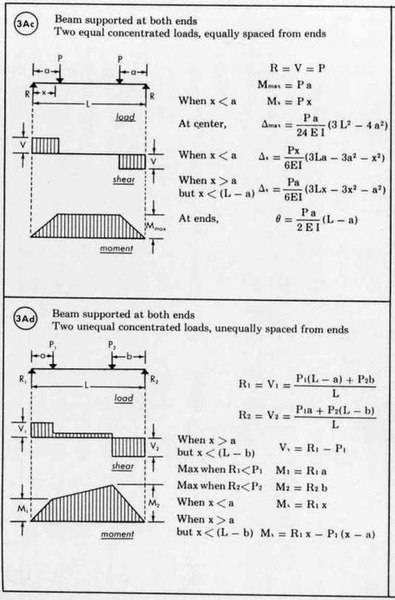
But again, they do not relate specifically to the mass system I am analysing with two overhanging masses.

So if anybody can help me out or atleast point me in the right direction as to how to calculate the deflections and the natural frequencies I would really appreciate it. Or even if there is a much better/more understandable way of doing this, I would love to hear about it. It's been years since I did engineering mechanics in college, and the cobwebs are impeding my memory!

Oh, by the way, I know it's quite a small system, and because of this I am expecting quite a high natural frequency! (Hopefully 1500Hz+)

All comments welcome!

EDIT: Sorry, I forgot to mention that I have the material properties and dimensions of the mass for (E,I...etc) for the deflection calculations. I just didn't post them as I would rather do the calculations myself if somebody could help me along the way!

 

[Navin A S]

Thanks! EDIT2: I have had a look at some other methods, such as Lagrange's equations, but they seem to be even more complicated than Rayleighs Energy Method (at least from what I can tell). So any help with the Rayleighs Method would be greatly appreciated!