- #1
mally baringon
- 2
- 0
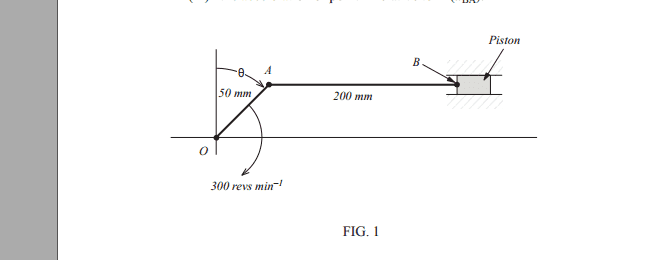
1. For the mechanism shown in FIGURE 1 determine for the angle
θ = 45°:
(i) the velocity of the piston relative to the fixed point O (VBO)
(ii) the angular velocity of AB about point A (i.e. ωAB)
(iii) the acceleration of point B relative to A (aBA).
(b) Determine the value of the angle θ (measured from vertical) when:
(i) the velocity of point B = 0
(ii) the angular velocity of link AB a maximum.
(c) What is the maximum angular velocity of link AB?
Vao = Loa x ωoa
Vao = Loa x ωoa = 0.005 x 10pi 0.1570
velocity triangle cosθ = Vbo/Vao
VBo =cos45 x Nao = 0.707 x 1.5708 = 1.1107 m/s^-1
I just have no idea where to start or what numbers to use where
θ = 45°:
(i) the velocity of the piston relative to the fixed point O (VBO)
(ii) the angular velocity of AB about point A (i.e. ωAB)
(iii) the acceleration of point B relative to A (aBA).
(b) Determine the value of the angle θ (measured from vertical) when:
(i) the velocity of point B = 0
(ii) the angular velocity of link AB a maximum.
(c) What is the maximum angular velocity of link AB?
Homework Equations
Vao = Loa x ωoa
The Attempt at a Solution
Vao = Loa x ωoa = 0.005 x 10pi 0.1570
velocity triangle cosθ = Vbo/Vao
VBo =cos45 x Nao = 0.707 x 1.5708 = 1.1107 m/s^-1
I just have no idea where to start or what numbers to use where