- #1
WWCY
- 479
- 12
HW Template missing as it was moved from another forum
Hi all,
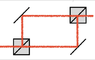
I have a problem trying to interpret the mathematics of this experiment and would like some help. I think it's best I write out all my ideas (and misconceptions) so that I can be corrected. An illustration of the setup is below. Thanks in advance for any assistance!
Let the following vectors represent "right-moving" and "upwards-moving" states of photons respectively
$$|r> \ = (1,0)$$
$$|u> \ = (0,1)$$
A beam of photons purely in the "right" state enters the first beam-splitter (represented by the matrix) and exits in a mix of "r" and "u" states
$$\frac{1}{\sqrt{2}}
\left( \begin{array}{cc}
1 & 1 \\
-1 & 1
\end{array} \right)
%
\left( \begin{array}{cc}
1 \\
0
\end{array} \right)
= \frac{1}{\sqrt{2}} \big ( (1,0) + (0,-1) \big)
$$
Assumption 1: ##\frac{1}{\sqrt{2}}(1,0)## represents the beam taking the right-wards path, and ##\frac{1}{\sqrt{2}}(0,-1)## is the beam moving upwards.
In the setup shown, both beams under go a "state-flip" as they hit the mirrors, and change direction and fly towards the second beam-splitter.
However, just for fun, I only want the "u" beam to hit a mirror, while the "r" beam just keeps flying right.
Assumption 2: I can do this by performing the "flip" on the "u" beam only. The "flipper" is represented by the matrix and the resulting state is
$$
\left( \begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array} \right)
%
\left( \begin{array}{cc}
0 \\
-\frac{1}{\sqrt{2}}
\end{array} \right)
= -\frac{1}{\sqrt{2}} (1,0)
$$
Assumption 3: Because both my beams are now "r" states, the probability of finding them as "r" states should be a sweet 1. And thus, summing the two "r-wards" vectors should give me ##(1,0)##. But
$$\frac{1}{\sqrt{2}} \big[ (1,0) + (-1,0) \big] = 0$$
Assumption 4: I could remove the negative sign from the "u" state vector, since the sign plays no physical significance. But this gives me ##\frac{1}{\sqrt{2}}(2,0)## which does not make sense either.
Assistance is greatly appreciated!
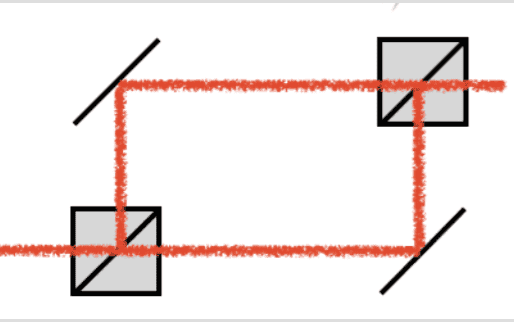
I have a problem trying to interpret the mathematics of this experiment and would like some help. I think it's best I write out all my ideas (and misconceptions) so that I can be corrected. An illustration of the setup is below. Thanks in advance for any assistance!
Let the following vectors represent "right-moving" and "upwards-moving" states of photons respectively
$$|r> \ = (1,0)$$
$$|u> \ = (0,1)$$
A beam of photons purely in the "right" state enters the first beam-splitter (represented by the matrix) and exits in a mix of "r" and "u" states
$$\frac{1}{\sqrt{2}}
\left( \begin{array}{cc}
1 & 1 \\
-1 & 1
\end{array} \right)
%
\left( \begin{array}{cc}
1 \\
0
\end{array} \right)
= \frac{1}{\sqrt{2}} \big ( (1,0) + (0,-1) \big)
$$
Assumption 1: ##\frac{1}{\sqrt{2}}(1,0)## represents the beam taking the right-wards path, and ##\frac{1}{\sqrt{2}}(0,-1)## is the beam moving upwards.
In the setup shown, both beams under go a "state-flip" as they hit the mirrors, and change direction and fly towards the second beam-splitter.
However, just for fun, I only want the "u" beam to hit a mirror, while the "r" beam just keeps flying right.
Assumption 2: I can do this by performing the "flip" on the "u" beam only. The "flipper" is represented by the matrix and the resulting state is
$$
\left( \begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array} \right)
%
\left( \begin{array}{cc}
0 \\
-\frac{1}{\sqrt{2}}
\end{array} \right)
= -\frac{1}{\sqrt{2}} (1,0)
$$
Assumption 3: Because both my beams are now "r" states, the probability of finding them as "r" states should be a sweet 1. And thus, summing the two "r-wards" vectors should give me ##(1,0)##. But
$$\frac{1}{\sqrt{2}} \big[ (1,0) + (-1,0) \big] = 0$$
Assumption 4: I could remove the negative sign from the "u" state vector, since the sign plays no physical significance. But this gives me ##\frac{1}{\sqrt{2}}(2,0)## which does not make sense either.
Assistance is greatly appreciated!