- #1
Waxterzz
- 82
- 0
Hi all,
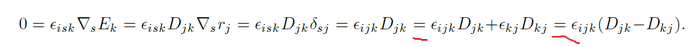
Can someone explain me the last two steps?
I don't know why suddenly there is a term with only two indices, and then in the last step you do something distributive and again three indices.
Thanks in advance
Can someone explain me the last two steps?
I don't know why suddenly there is a term with only two indices, and then in the last step you do something distributive and again three indices.
Thanks in advance