- #1
stef6987
- 32
- 0
1. Homework Statement [/b]
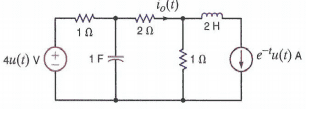
I'm required to find the current i0(t), i wrote KVL equations for each loop, I0 can be expressed interms of i1 and i3, i3 being the current source on the right. i managed to get the solution down to the following :
i0 = (s + 4)/(3*s^2 + 4*s + 1)
I simplified the denominator by completing the square and got:
i0 = (s + 4)/((3*(s+4/6)^2 - 12/36))
Now I'm kind of stuck, i one of solutions is in the form (s+a)/((s+a)^2 + w^2) I'm not sure how i can get my solution to be similar to this, any tips would be awesome :)
thankyou!
I'm required to find the current i0(t), i wrote KVL equations for each loop, I0 can be expressed interms of i1 and i3, i3 being the current source on the right. i managed to get the solution down to the following :
i0 = (s + 4)/(3*s^2 + 4*s + 1)
I simplified the denominator by completing the square and got:
i0 = (s + 4)/((3*(s+4/6)^2 - 12/36))
Now I'm kind of stuck, i one of solutions is in the form (s+a)/((s+a)^2 + w^2) I'm not sure how i can get my solution to be similar to this, any tips would be awesome :)
thankyou!