- #1
Happiness
- 679
- 30
Why do displaced paths need to satisfy the equations of constraint when using the method of Lagrange multiplier? I thought that with the multiplier, all the coordinates are free and hence should not be required to satisfy the equations of constraint.
Source: http://www.phys.ufl.edu/~maslov/classmech/flannery.pdf


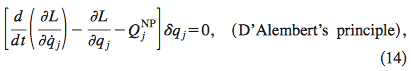

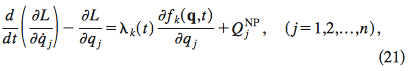
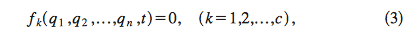

Source: http://www.phys.ufl.edu/~maslov/classmech/flannery.pdf