- #1
piercazzo
- 1
- 0
I have a rotated ellipse, not centered at the origin, defined by x,y,a,b and angle.
Then I have a segment defined by two points x1,y1 and x2,y2
Is there a quick way to find the intersection points?
I used wolfram alpha equation solver, I tried to insert the equation of a line into the one of a standard non rotated, non translated ellipse,
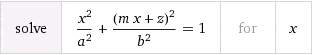
and resolving for x this is the result
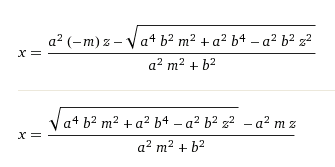
which is nice.
Then I took the equation of a rotated and translated ellipse
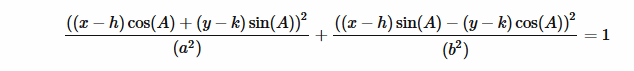
and this is the result
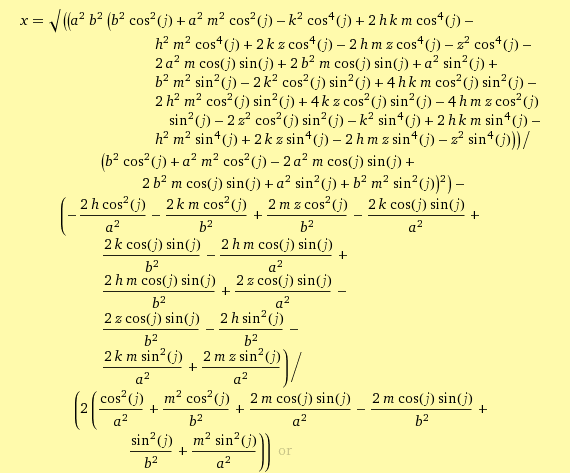

Which is obviously impractical, can anyone suggest a different method?
Then I have a segment defined by two points x1,y1 and x2,y2
Is there a quick way to find the intersection points?
I used wolfram alpha equation solver, I tried to insert the equation of a line into the one of a standard non rotated, non translated ellipse,
and resolving for x this is the result
which is nice.
Then I took the equation of a rotated and translated ellipse
and this is the result
Which is obviously impractical, can anyone suggest a different method?